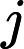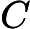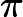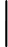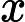Sie stellen wirklich zwei verschiedene Fragen und hoffen, dass es eine einzige Antwort gibt, die beide beantwortet: (1) Welche natürlichen Vorstellungen von quantenmonotonen Schaltkreisen gibt es? (2) Wie würde ein gitterbasiertes Quantenergebnis im Razborov-Stil aussehen?
Es ist nicht offensichtlich, wie beides gleichzeitig erreicht werden kann, daher beschreibe ich, was für mich eine vernünftige Vorstellung von monotonen Quantenschaltungen ist (ohne anzugeben, ob es ein entsprechendes Razborov-Ergebnis gibt oder nicht), und eine völlig andere Vorstellung von wie eine "natürliche" Quanten-Razborov-Vermutung aussehen würde (ohne anzugeben, ob es wahrscheinlich wahr ist).
Was wir von Quanten wollen
Wie ich in den Kommentaren bemerkte, denke ich, dass es nicht notwendig ist, den Begriff der monotonen Schaltkreise in eine Form der Einheitlichkeit zu bringen. Ob es nun darum geht, dass die zeitliche Entwicklung nicht die Standardbasis bewahren muss oder dass es mehrere Messgrundlagen gibt, in die die Ergebnisse verwickelt sein können, ich denke, die unabdingbare Voraussetzung für die Quantenberechnung ist die Tatsache, dass die Standardbasis ist nicht die einzige Basis. Sogar unter den Produktzuständen wird es in einigen Implementierungen nur durch eine Wahl des Bezugsrahmens definiert.
Was wir tun müssen, ist, die Dinge so zu betrachten, dass die Standardbasis von ihrem traditionellen privilegierten Platz entfernt wird - oder in diesem Fall so weit wie möglich, während ein bedeutungsvoller Begriff von Monotonie beibehalten wird.
Ein einfaches Modell von monotonen Quantenschaltungen
Betrachten Sie ein Schaltungsmodell, das in Tsuyoshi Itos Kommentar über "monotone Quantenkanäle" impliziert ist (und das so ziemlich das ist, was man tun muss, wenn man einen Begriff von "einer Schaltung" haben möchte, der nicht auf die einheitliche Evolution beschränkt ist).
Sei der Raum der Hermitianischen Operatoren auf (so dass er alle Dichteoperatoren auf einem Qubit enthält). Wie definieren wir ein Quantenmonoton-Gatter von zwei Eingangs-Qubits bis zu einem Ausgangs-Qubit , so dass es kein klassisches ist monotones Tor? Ich denke, es ist einfach zu sagen, dass die Ausgabe nicht aufoderoder Mischungen davon; Wenn dies "monoton" sein soll, sollten wir dies als fordern und C 2 G : H a ⊗ H b → H c a , b c | 0 ⟩















 | 1 ⟩
| 1 ⟩




 ⟨ 1 |
⟨ 1 |




 ⟨1|
⟨1|









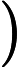


 ⟨1| G(ρ a b )| 1⟩G
⟨1| G(ρ a b )| 1⟩G











 erhöhe den Wert von darf nicht abnehmen. Für ein Qubit-Gatter mit zwei Eingängen bedeutet dies, dass im Prinzip wie implementierbar sein muss
erhöhe den Wert von darf nicht abnehmen. Für ein Qubit-Gatter mit zwei Eingängen bedeutet dies, dass im Prinzip wie implementierbar sein muss












Durchführen einer Zwei-Qubit-Messung in Bezug auf eine orthonormale Basis , wobei überspanne den Unterraum von Hamminggewicht 1 und| & mgr; ⟩ , | & ngr; ⟩

























Als Ausgabe wird ein Zustand , der dem gemessenen Ergebnis entspricht, wobei für jedes .



















































Die Schaltkreise sind sinnvollerweise nur Kompositionen davon. Wir könnten auch Fan-Out in Form von Schaltkreisen zulassen, die einheitlich und einbetten ; Wir sollten diese Maps zumindest am Eingang zulassen, damit jedes (nominell klassische) Eingabebit kopiert werden kann.



















Es erscheint vernünftig, entweder das gesamte Kontinuum solcher Tore zu betrachten oder sich auf eine begrenzte Sammlung solcher Tore zu beschränken. Jede Wahl führt zu einer anderen "Quantenmonoton-Gate-Basis" für die Schaltungen; man kann überlegen, welche Eigenschaften verschiedene monotone Basen haben. Die Zustände können unter Berücksichtigung der Monotoniebedingung völlig unabhängig voneinander ausgewählt werden. Es wäre zweifellos interessant (und wahrscheinlich praktisch, Fehler zu binden),und, obwohl ich keinen Grund sehe, dies in der Theorie zu fordern. Offensichtlich sind AND und OR Tore dieses Typs, bei denenund























































 jeweils, was auch immer man wählt, um oder zu sein.
jeweils, was auch immer man wählt, um oder zu sein.





Für jede Konstante k könnte man auch Gate-Basen in Betracht ziehen, einschließlich k- Input-One-Output-Gates. Der einfachste Ansatz in diesem Fall wäre wahrscheinlich, Gates zuzulassen, was wie oben implementiert werden kann, was jede Zerlegung der Teilräume jedes Hamming-Gewichts , und zu fordern, dass
für jeden





































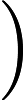



















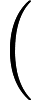






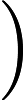








. Es ist nicht klar, wie viel zusätzliche Rechenleistung Ihnen dies geben würde (auch nicht im klassischen Fall).
Ich weiß nicht, ob es etwas Interessantes gibt, über solche Schaltkreise jenseits des klassischen Falls zu sagen, aber dies scheint mir die vielversprechendste Kandidatendefinition eines "Quantenmonoton-Schaltkreises" zu sein.
Eine Quantenvariante von Rasborows Ergebnis
Betrachten Sie die Darstellung der Ergebnisse von Alon & Boppana (1987), Combinatorica 7, S. 1–22 durch Tim Gowers , die Razborovs Ergebnisse für die monotone Komplexität von CLIQUE stärken (und einige seiner Techniken explizit machen). Gowers stellt dies in Form einer rekursiven Konstruktion einer , die aus den "Halbräumen" des Booleschen Würfels für jedes . Wenn wir die privilegierte Position der Standardbasis in den Basissätzen entfernen , können wir in Analogie zum Quantum Lovász Local Lemma einen Unterraum von


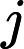






einem binären Satz zu entsprechen (ob ein Zustand zum Unterraum gehört oder stattdessen orthogonal dazu ist), der sich aus der Messung ergeben könnte. Zum Beispiel können wir Teilräume die durch
Wir erlauben die
quantenlogischen Analoga der Konjunktion und Disjunktion von Subspaces:


































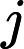




























































































Wir fragen dann, wie lange eine rekursive Konstruktion von Konjunktionen und Disjunktionen von Räumen erforderlich ist, um einen Raum , so dass sich der Projektor auf nur geringfügig vom Projektor auf den durch die Indikatorfunktionen von Graphen mit Cliquen der Größe aufgespannten Raum ; zum Beispiel, damit


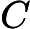









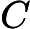


















. Der monotone Teil ist an den quantenlogischen Operationen beteiligt, und die primitiven Aussagen über die Eingabe sind ebenfalls Quanten.
Im allgemeinen Fall besteht ein Problem darin, dies als Rechenproblem zu behandeln: Die Disjunktion entspricht keinem Wissen, das mit Sicherheit durch Messungen an einer begrenzten Anzahl von Kopien unter Verwendung von Black-Box-Messungen für und allein, es sei denn, es handelt sich um Bilder von Pendelprojektoren. Dieses allgemeine Problem kann immer noch als interessantes Ergebnis der geometrisch-kombinatorischen Komplexität betrachtet werden und kann zu Ergebnissen führen, die mit frustrierten lokalen Hamiltioniern zusammenhängen. Es könnte jedoch natürlicher sein, nur die Subspaces


 entstehen durch Pendeln von Projektoren. In diesem Fall ist die Disjunktion nur der klassische ODER der Messergebnisse dieser Projektoren. Dann können wir verlangen, dass die Unitaries alle gleich sind, und dies wird zu einem Problem in eine Unitary Circuit (die die "primitiven Ereignisse" hervorruft) mit monotoner klassischer Nachbearbeitung (die die logischen Operationen für diese Ereignisse ausführt).
entstehen durch Pendeln von Projektoren. In diesem Fall ist die Disjunktion nur der klassische ODER der Messergebnisse dieser Projektoren. Dann können wir verlangen, dass die Unitaries alle gleich sind, und dies wird zu einem Problem in eine Unitary Circuit (die die "primitiven Ereignisse" hervorruft) mit monotoner klassischer Nachbearbeitung (die die logischen Operationen für diese Ereignisse ausführt).

Beachten Sie auch, dass, wenn wir keine weiteren Einschränkungen für die Leerzeichen , dies ein Unterraum mit sehr großer Überlappung mit einigen Leerzeichen , die von den Standardbasiszuständen werden. Welches sind die binären Zeichenfolgen, in denen .













Wenn diese Möglichkeit macht squeamish, kann man immer , dass erfordern hat einen Winkel von Trennung von jedem mindestens (damit unsere primitiven Unterräume im schlimmsten Fall in etwa unabhängig von den Unterräumen sind, in denen eines der Bits auf 1 gesetzt ist).




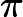











Wenn wir keine solche Einschränkung auferlegen, scheint es mir ohnehin ein Hindernis für die Annäherung an CLIQUE (r) zu sein, wenn Subspaces mit hoher Überlappung mit werden; Entweder wären wir mehr oder weniger darauf beschränkt, das Fehlen einer bestimmten Kante (und nicht deren Vorhandensein) zu berücksichtigen , oder wir wären gezwungen, eine der Kanten insgesamt zu ignorieren. Daher halte ich es nicht für furchtbar wichtig, irgendwelche Einschränkungen , außer möglicherweise, dass sie alle die Bilder eines pendelnden Satzes von Projektoren sind, wenn man , wie man CLIQUE aus einfachen Quantensätzen monoton auswertet ". Im schlimmsten Fall würde dies klassisch bedeuten, NICHT-Gatter am Eingang zuzulassen (und alle Fan-Outs nach der Negation zuzulassen).




Auch hier ist mir nicht klar, ob das Ersetzen der Basismengen durch beliebige Unterräume von zu einem interessanteren Problem führt als nur die Verwendung der Unterräume ; Wenn wir uns jedoch auf den Fall von CNF-Formeln beschränken (entweder im Fall des Pendelns oder im Fall des Nicht-Pendelns), würden die Ergebnisse einer Vorstellung von der Komplexität eines frustrationsfreien Hamiltonianers entsprechen, dessen Grundzustandsvielfalt aus einer Standardbasis bestand Staaten, die Cliquen vertreten.