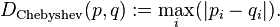Wie kann man die Distanzfunktion optimieren?

Während ich ein relativ einfaches RTS-ähnliches Spiel entwickelte, bemerkte ich, dass meine Entfernungsberechnungen die Leistung beeinträchtigten.

Zu jeder Zeit werden Entfernungsprüfungen durchgeführt, um festzustellen, ob sich eine Einheit in Reichweite des Ziels befindet, ob das Projektil das Ziel erreicht hat, ob der Spieler einen Pickup, eine allgemeine Kollision usw. überfahren hat. Die Liste wird fortgesetzt und nachgeprüft Abstand zwischen zwei Punkten wird häufig verwendet.

Genau darum geht es bei meiner Frage. Ich möchte wissen, welche Alternativen Spieleentwickler haben, um Entfernungen zu überprüfen, abgesehen von dem üblichen sqrt (x * x + y * y) -Ansatz, der ziemlich zeitaufwendig ist, wenn wir ihn tausende Male pro Frame ausführen.

Ich möchte darauf hinweisen, dass mir die Entfernungen in Manhattan und die Entfernungsvergleiche im Quadrat bekannt sind (indem ich den sqrt-Engpass überspringe). Noch etwas?

TL; DR; Ihr Problem besteht nicht in der Ausführung der Distanzfunktion. Ihr Problem besteht darin, die Distanzfunktion so oft auszuführen. Mit anderen Worten, Sie benötigen eher eine algorithmische Optimierung als eine mathematische.

[EDIT] Ich lösche den ersten Teil meiner Antwort, weil die Leute es hassen. Der Fragentitel verlangte vor der Bearbeitung nach alternativen Entfernungsfunktionen.

Sie verwenden eine Distanzfunktion, bei der Sie jedes Mal die Quadratwurzel berechnen. Sie können dies jedoch einfach ersetzen, ohne die Quadratwurzel zu verwenden, und stattdessen den quadratischen Abstand berechnen. Dies erspart Ihnen viele wertvolle Zyklen.

Abstand ^ 2 = x * x + y * y;

das ist eigentlich ein üblicher trick. Sie müssen jedoch Ihre Berechnungen entsprechend anpassen. Sie kann auch als Erstprüfung vor der Berechnung der tatsächlichen Entfernung verwendet werden. Anstatt zum Beispiel den tatsächlichen Abstand zwischen zwei Punkten / Kugeln für einen Schnittpunkttest zu berechnen, können wir stattdessen den quadratischen Abstand berechnen und mit dem quadratischen Radius anstelle des Radius vergleichen.

Bearbeiten Sie, nachdem @ Byte56 darauf hingewiesen hat, dass ich die Frage nicht gelesen habe und dass Sie sich der Quadratabstandsoptimierung bewusst waren.

Nun, in Ihrem Fall beschäftigen wir uns leider in der Computergrafik fast ausschließlich mit dem euklidischen Raum , und die Entfernung ist genau wie Sqrt of Vector dot itselfim euklidischen Raum definiert.

Das Quadrat der Entfernung ist die beste Annäherung, die Sie erhalten werden (in Bezug auf die Leistung). Ich kann nichts sehen, das 2 Multiplikationen, eine Addition und eine Zuweisung schlägt.

Sie sagen also, ich kann die Distanzfunktion nicht optimieren. Was soll ich tun?

Ihr Problem besteht nicht in der Ausführung der Distanzfunktion. Ihr Problem besteht darin, die Distanzfunktion so oft auszuführen. Mit anderen Worten, Sie benötigen eher eine algorithmische Optimierung als eine mathematische.

Der Punkt ist, anstatt die Schnittmenge des Spielers mit jedem Objekt in der Szene zu überprüfen, jedes Bild. Sie können die räumliche Kohärenz problemlos zu Ihrem Vorteil nutzen und nur die Objekte überprüfen, die sich in der Nähe des Players befinden (die am wahrscheinlichsten treffen / sich schneiden).

Dies kann leicht erreicht werden, indem diese räumlichen Informationen tatsächlich in einer räumlichen Partitionierungsdatenstruktur gespeichert werden . Für ein einfaches Spiel würde ich ein Grid vorschlagen, da es im Grunde einfach zu implementieren ist und sich gut in eine dynamische Szene einfügt.

Jede Zelle / Box enthält eine Liste von Objekten, die vom Begrenzungsrahmen des Gitters eingeschlossen werden. Und es ist einfach, die Position des Spielers in diesen Zellen zu verfolgen. Und für die Entfernungsberechnung überprüfen Sie nur die Spielerentfernung mit diesen Objekten innerhalb derselben oder benachbarter Zellen anstelle von allem in der Szene.

Ein komplizierterer Ansatz ist die Verwendung von BSP oder Octrees.

Wenn Sie etwas benötigen, das über eine beliebige Distanz linear bleibt (im Gegensatz zu distance^2) und dennoch vage kreisförmig erscheint (im Gegensatz zu den quadratischen Abständen von Chebyshev und Manhattan), können Sie die beiden letztgenannten Techniken mitteln, um eine achteckige Distanznäherung zu erhalten:

dx = abs(x1 - x0)
dy = abs(y1 - y0)

dist = 0.5 * (dx + dy + max(dx, dy))

Hier eine Visualisierung (Konturdiagramm) der Funktion dank Wolfram Alpha :

Und hier ist eine grafische Darstellung der Fehlerfunktion im Vergleich zum euklidischen Abstand (Bogenmaß, nur erster Quadrant):

Wie Sie sehen können, reicht der Fehler von 0% auf den Achsen bis ungefähr + 12% in den Lappen. Wenn wir die Koeffizienten ein wenig verändern, können wir sie auf +/- 4% senken:

dist = 0.4 * (dx + dy) + 0.56 * max(dx, dy)

Aktualisieren

Unter Verwendung der obigen Koeffizienten liegt der maximale Fehler innerhalb von +/- 4%, der durchschnittliche Fehler beträgt jedoch immer noch + 1,3%. Optimiert für den Nulldurchschnittsfehler können Sie Folgendes verwenden:

dist = 0.394 * (dx + dy) + 0.554 * max(dx, dy)

was zu Fehlern zwischen -5% und + 3% und einem durchschnittlichen Fehler von + 0,043% führt

Während ich im Web nach einem Namen für diesen Algorithmus suchte, fand ich diese ähnliche achteckige Annäherung :

dist = 1007/1024 * max(dx, dy) + 441/1024 * min(dx, dy)

Beachten Sie, dass dies im Wesentlichen äquivalent ist (obwohl die Exponenten unterschiedlich sind - diese geben einen Fehler von -1,5% bis 7,5%, aber es kann auf +/- 4% massiert werden), weil max(dx, dy) + min(dx, dy) == dx + dy. Mit diesem Formular können die Aufrufe minund maxzugunsten von:

if (dy > dx)
    swap(dx, dy)

dist = 1007/1024 * dx + 441/1024 * dy

Wird das schneller sein als meine Version? Wer weiß ... hängt vom Compiler ab und davon, wie er jeden für die Zielplattform optimiert. Meiner Meinung nach ist es ziemlich schwierig, einen Unterschied zu erkennen.

Manchmal kann diese Frage nicht aufgrund der Kosten für die Durchführung von Entfernungsberechnungen auftreten, sondern aufgrund der Häufigkeit, mit der die Berechnung durchgeführt wird.

In einer großen Spielwelt mit vielen Akteuren ist es nicht skalierbar , den Abstand zwischen einem und allen anderen Akteuren zu überprüfen. Je mehr Spieler, NSCs und Projektile auf der Welt sind, desto mehr Vergleiche müssen im gleichen Maße durchgeführt werden O(N^2).

Eine Möglichkeit, dieses Wachstum zu reduzieren, besteht darin, eine gute Datenstruktur zu verwenden, um unerwünschte Akteure schnell aus den Berechnungen zu streichen.

Wir suchen nach einer Möglichkeit, alle Akteure, die sich möglicherweise in Reichweite befinden, effizient zu iterieren, wobei wir die Mehrheit der Akteure ausschließen, die definitiv außerhalb der Reichweite liegen .

Wenn Ihre Schauspieler ziemlich gleichmäßig über den Weltraum verteilt sind, sollte ein Gitter von Eimern eine geeignete Struktur sein (wie die akzeptierte Antwort nahelegt). Indem Sie Verweise auf Akteure in einem groben Raster beibehalten, müssen Sie nur einige der in der Nähe befindlichen Bereiche überprüfen, um alle Akteure abzudecken, die sich in Reichweite befinden könnten, und den Rest ignorieren. Wenn ein Schauspieler umzieht, müssen Sie ihn möglicherweise von seinem alten in einen neuen Eimer umziehen.

Für Schauspieler, die weniger gleichmäßig verteilt sind, ist ein Quadtree möglicherweise besser für eine zweidimensionale Welt geeignet , oder ein Octree ist für eine dreidimensionale Welt geeignet. Dies sind allgemeinere Strukturen, die große Bereiche des leeren Raums und kleine Bereiche mit vielen Akteuren effizient unterteilen können. Für statische Akteure gibt es eine binäre Raumpartitionierung ( Binary Space Partitioning, BSP), die sehr schnell zu suchen ist, aber viel zu teuer, um sie in Echtzeit zu aktualisieren. BSPs trennen den Raum mithilfe von Ebenen, um ihn wiederholt zu halbieren, und können auf eine beliebige Anzahl von Dimensionen angewendet werden.

Natürlich gibt es Overheads, um Ihre Akteure eine solche Struktur zu halten, besonders wenn sie sich zwischen Partitionen bewegen. Aber in einer großen Welt mit vielen Akteuren, aber kleinen Interessensbereichen, sollten die Kosten weitaus niedriger sein als diejenigen, die durch einen naiven Vergleich mit allen Objekten entstehen.

Die Überlegung, wie die Kosten eines Algorithmus steigen, wenn er mehr Daten empfängt, ist für das skalierbare Softwaredesign von entscheidender Bedeutung. Manchmal reicht es aus, einfach die richtige Datenstruktur zu wählen . Die Kosten werden normalerweise in der Big O-Notation angegeben .

(Mir ist klar, dass dies keine direkte Antwort auf die Frage ist, aber es kann für einige Leser nützlich sein. Ich entschuldige mich, wenn ich Ihre Zeit verschwendet habe!)

Wie wäre es mit der Chebyshev Entfernung? Für die Punkte p, q ist es wie folgt definiert:

Für die Punkte (2, 4) und (8, 5) beträgt der Chebyshev-Abstand 6 als | 2-8 | > | 4-5 |.

Weiterhin sei E die euklidische Distanz und C die Chebyshev-Distanz. Dann:

Die obere Schranke ist wahrscheinlich nicht sehr nützlich, da Sie die Quadratwurzel berechnen müssten, aber die untere Schranke könnte hilfreich sein - wenn der Chebyshev-Abstand groß genug ist, um außerhalb des Bereichs zu liegen, muss der euklidische Abstand ebenfalls vorhanden sein, um Sie zu retten von der Notwendigkeit, es zu berechnen.

Der Nachteil ist natürlich, dass Sie, wenn sich die Chebyshev-Entfernung in Reichweite befindet, die euklidische Entfernung ohnehin berechnen müssen, was Zeit verschwendet. Nur ein Weg, um herauszufinden, ob es ein Nettogewinn sein wird!

Eine sehr einfache lokale Optimierung besteht darin, zunächst nur eine Dimension zu überprüfen.

Das ist :

distance ( x1, y1 , x1, y2) > fabs (x2 - x1)

Wenn Sie also nur fabs (x2 - x1)als ersten Filter prüfen , erhalten Sie möglicherweise einen spürbaren Gewinn. Wie viel davon abhängt, hängt von der Größe der Welt im Vergleich zu den relevanten Bereichen ab.

Darüber hinaus können Sie dies als Alternative zur räumlichen Partitionierungsdatenstruktur verwenden.

Wenn alle relevanten Objekte in einer Liste in x-Koordinatenreihenfolge sortiert sind, müssen sich Objekte in der Nähe in der Liste befinden. Selbst wenn die Liste nicht mehr in Ordnung ist, weil Objekte nicht mehr vollständig gewartet werden, können Sie bei bekannten Geschwindigkeitsgrenzen den zu durchsuchenden Teil der Liste nach Objekten in der Nähe verkleinern.

In der Vergangenheit wurden Anstrengungen zur Optimierung unternommen sqrt. Obwohl es für heutige Maschinen nicht mehr gilt, ist hier ein Beispiel aus dem Quake-Quellcode, der die magische Zahl verwendet 0x5f3759df :

float Q_rsqrt( float number )
{
  long i;
  float x2, y;
  const float threehalfs = 1.5F;

  x2 = number * 0.5F;
  y  = number;
  i  = * ( long * ) &y;  // evil floating point bit level hacking
  i  = 0x5f3759df - ( i >> 1 ); // what the hell?
  y  = * ( float * ) &i;
  y  = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration
  // y  = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration (optional)
  // ...
  return y;
}

Eine ausführliche Erklärung der Vorgänge finden Sie auf Wikipedia.

Kurz gesagt, es sind einige Iterationen der Newtonschen Methode (ein numerischer Algorithmus, der eine Schätzung iterativ verbessert), wobei die magische Zahl verwendet wird, um eine vernünftige anfängliche Schätzung bereitzustellen.

Travis weist darauf hin, dass diese Art der Optimierung für moderne Architekturen nicht mehr sinnvoll ist. Und selbst wenn dies der Fall wäre, könnte Ihr Engpass nur mit einer konstanten Geschwindigkeit beschleunigt werden, während eine algorithmische Neugestaltung möglicherweise bessere Ergebnisse erzielt.