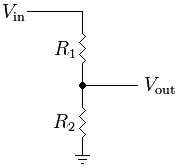
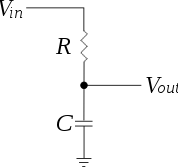
Zu der Frage "Was ist Impedanz?" Möchte ich bemerken, dass Impedanz ein allgemeines Konzept der Physik ist, für das die elektrische Impedanz nur ein Beispiel ist.
Um zu verstehen, was es bedeutet und wie es funktioniert, ist es oft einfacher, stattdessen die mechanische Impedanz zu berücksichtigen. Denken Sie daran, eine schwere Couch über den Boden zu schieben.
Sie üben eine bestimmte Kraft aus und die Couch gleitet mit einer bestimmten Geschwindigkeit. Dies hängt davon ab, wie stark Sie drücken, wie schwer die Couch ist, welche Art von Bodenfläche und welche Art von Füßen die Couch hat und so weiter. In dieser Situation kann eine mechanische Impedanz definiert werden, die das Verhältnis zwischen dem Druck und der Geschwindigkeit der Liege angibt.
Dies ähnelt einem elektrischen Gleichstromkreis, bei dem eine bestimmte Spannung an einen Stromkreis angelegt wird und der Strom mit einer bestimmten entsprechenden Rate durch den Stromkreis fließt.
Sowohl für die Liege als auch für den Stromkreis kann die Reaktion auf Ihre Eingabe einfach und ziemlich linear sein: ein Widerstand, der dem Ohmschen Gesetz entspricht, wobei seine elektrische Impedanz nur der Widerstand ist, und die Liege kann Gleitfüße mit Reibung aufweisen, die dies ermöglichen mit einer Geschwindigkeit bewegen, die proportional zu Ihrer Kraft ist. *
Schaltungen und mechanische Systeme können auch nichtlinear sein. Wenn Ihre Schaltung aus einer variablen Spannung besteht, die über einen Widerstand in Reihe mit einer Diode gelegt wird, ist der Strom nahe Null, bis Sie die Durchlassspannung der Diode überschreiten. An diesem Punkt beginnt der Strom gemäß Ohm durch den Widerstand zu fließen Gesetz. Ebenso hat eine auf dem Boden sitzende Couch in der Regel eine gewisse Haftreibung: Sie bewegt sich erst, wenn Sie mit einer bestimmten Anfangskraft drücken. Weder im mechanischen noch im elektrischen System gibt es eine einzige lineare Impedanz, die definiert werden kann. Das Beste, was Sie tun können, ist, die Impedanzen unter verschiedenen Bedingungen separat zu definieren. (Die reale Welt ist viel mehr so.)
Selbst wenn die Dinge sehr klar und linear sind, ist es wichtig zu beachten, dass die Impedanz nur ein Verhältnis beschreibt - es beschreibt nicht die Grenzen des Systems und es ist nicht "schlecht". Sie können definitiv so viel Strom / Geschwindigkeit erhalten, wie Sie möchten (in einem idealen System), indem Sie mehr Spannung hinzufügen / stärker drücken.
Mechanische Systeme können auch ein ziemlich gutes Gefühl für die Wechselstromimpedanz geben. Stellen Sie sich vor, Sie fahren Fahrrad. Mit jedem halben Pedalzyklus drückst du nach links, drückst nach rechts. Sie können sich auch vorstellen, mit nur einem Fuß und einem Zehenclip in die Pedale zu treten, sodass Sie bei jedem Pedalzyklus drücken und ziehen. Dies ähnelt dem Anlegen einer Wechselspannung an einen Stromkreis: Sie drücken und ziehen abwechselnd zyklisch mit einer bestimmten Frequenz.
Wenn die Frequenz langsam genug ist - wie beim Anhalten auf dem Fahrrad -, ist das Problem des Herunterdrückens der Pedale nur ein "Gleichstrom" -Problem, wie das Drücken der Couch. Wenn Sie jedoch beschleunigen, können sich die Dinge anders verhalten.
Angenommen, Sie fahren mit einer bestimmten Geschwindigkeit und Ihr Fahrrad hat drei Gänge mit niedrigen, mittleren und hohen Übersetzungsverhältnissen. Medium fühlt sich natürlich an, Hi-Gear ist schwierig genug Kraft anzuwenden, um einen Unterschied zu machen, und bei niedrigem Gang treten Sie einfach in die Pedale, ohne Energie auf die Räder zu übertragen. Hierbei handelt es sich um eine Impedanzanpassung , bei der Sie die Kraft nur dann effektiv auf die Räder übertragen können, wenn sie Ihrem Fuß einen gewissen physischen Widerstand entgegensetzen - nicht zu viel, nicht zu wenig. Das entsprechende elektrische Phänomen ist ebenfalls sehr häufig; Sie benötigen impedanzangepasste Leitungen, um die HF-Leistung effektiv von Punkt A nach Punkt B zu übertragen. Jedes Mal, wenn Sie zwei Übertragungsleitungen miteinander verbinden, tritt an der Schnittstelle ein Verlust auf.
Der Widerstand, den die Pedale auf Ihre Füße ausüben, ist proportional zum Druck, was einem einfachen Widerstand am ehesten entspricht - insbesondere bei niedrigen Geschwindigkeiten. Auch in Wechselstromkreisen verhält sich ein Widerstand (bis zu einem bestimmten Punkt) wie ein Widerstand.
Im Gegensatz zu einem Widerstand ist die Impedanz eines Fahrrads jedoch von der Frequenz abhängig. Stellen Sie sich vor, Sie legen einen hohen Gang ein und beginnen bei einem Stopp. Der Einstieg kann sehr schwierig sein. Aber sobald Sie anfangen, sinkt die Impedanz der Pedale, wenn Sie schneller werden, und wenn Sie sehr schnell fahren, stellen Sie möglicherweise fest, dass die Pedale eine zu geringe Impedanz aufweisen, um die Kraft von Ihren Füßen zu absorbieren. Es gibt also tatsächlich eine frequenzabhängige Impedanz (eine Reaktanz ), die hoch beginnt und niedriger wird, wenn Sie zu einer höheren Frequenz gehen.
Dies ist dem Verhalten eines Kondensators sehr ähnlich, und ein ziemlich gutes Modell für die mechanische Impedanz eines Fahrrads wäre ein Widerstand parallel zu einem Kondensator.
Bei Gleichstrom (Geschwindigkeit Null) sehen Sie nur den hohen, konstanten Widerstand als Ihre Impedanz. Mit zunehmender Trittfrequenz wird die Kondensatorimpedanz niedriger als die des Widerstands und lässt den Strom auf diese Weise fließen.
Es gibt natürlich verschiedene andere elektrische Komponenten und ihre mechanischen Analogien **, aber diese Diskussion soll Ihnen eine erste Vorstellung vom allgemeinen Konzept vermitteln, wie Sie geerdet bleiben (Wortspiel beabsichtigt), wenn Sie sich mit den mathematischen Aspekten dessen befassen, was manchmal scheinen kann wie ein sehr abstraktes Thema.
* Ein Wort zu den Wählerischen: Das Ohmsche Gesetz ist für ein reales Gerät niemals exakt, und Reibungskräfte aus der realen Welt geben niemals eine Geschwindigkeit an, die genau proportional zur Kraft ist. "Ziemlich linear" ist jedoch einfach. Ich versuche hier alles zu lernen und so. Schneiden Sie mich etwas lockerer.
** Ein Induktor ist beispielsweise eine federbelastete Rolle auf Ihrem Rad, die den Luftwiderstand erhöht, wenn Sie eine höhere Frequenz erreichen.)