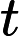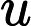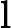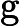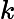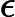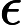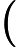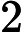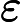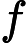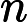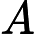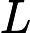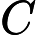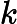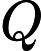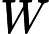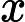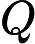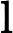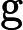Nach Ladners Theorem gibt es unendlich viele N P -Intermediat- ( N P I ) -Probleme , wenn ist . Es gibt auch natürliche Kandidaten für diesen Status, wie zum Beispiel Graph Isomorphism, und eine Reihe anderer, siehe Probleme zwischen P und NPC . Dennoch ist die überwiegende Mehrheit in der Menge der bekannten n ein t u r ein l N P ist bekannt -Probleme entweder in seine P oder N P C . Nur ein kleiner Teil von ihnen bleibt ein Kandidat für die N P I . Mit anderen Worten, wenn wir zufällig ein natürliches -Problem unter den bekannten auswählen, haben wir sehr wenig Chance, einen N P I -Kandidaten auszuwählen . Gibt es eine Erklärung für dieses Phänomen?
Ich könnte mir 3 mögliche Erklärungen ausdenken, mehr auf der philosophischen Seite:
Der Grund für einen so geringen Anteil an natürlichen -Kandidaten ist, dass sich N P I letztendlich als leer herausstellen wird. Ich weiß, das impliziert P = N P , also ist es sehr unwahrscheinlich. Dennoch könnte man noch streiten (obwohl ich nicht einer von ihnen bin) , dass die Seltenheit der natürlichen N P I Probleme ist eine empirische Beobachtung , dass erscheint tatsächlich zur Unterstützung P = N P , im Gegensatz zu den meisten anderen Beobachtungen.
Die Kleinheit von "natural- " stellt eine Art scharfen Phasenübergang zwischen einfachen und harten Problemen dar. Anscheinend verhalten sich die bedeutungsvollen, natürlichen algorithmischen Probleme so, dass sie entweder einfach oder schwierig sind. Der Übergang ist eng (aber immer noch vorhanden).
Das Argument in 2 kann auf die Spitze getrieben werden: schließlich alle Probleme in "natur- " wird in gesetzt werden P ∪ N P C , noch P ≠ N P , so N P I ≠ ∅ . Dies würde bedeuten, dass alle verbleibenden Probleme in N P I sindsind "unnatürlich" (erfunden, ohne realen Sinn). Eine Interpretation davon könnte sein, dass natürliche Probleme entweder leicht oder schwer sind; der Übergang ist nur ein logisches Konstrukt ohne "physikalische" Bedeutung. Dies erinnert ein wenig an irrationale Zahlen, die durchaus logisch sind, aber nicht als Messwert einer physikalischen Größe auftreten. Als solche kommen sie nicht aus der physischen Realität, sondern befinden sich im "logischen Verschluss" dieser Realität.
Welche Erklärung magst du am liebsten oder kannst du eine andere vorschlagen?