Kann der Teilungsschritt in einer Zusammenführungssorte vermieden werden?

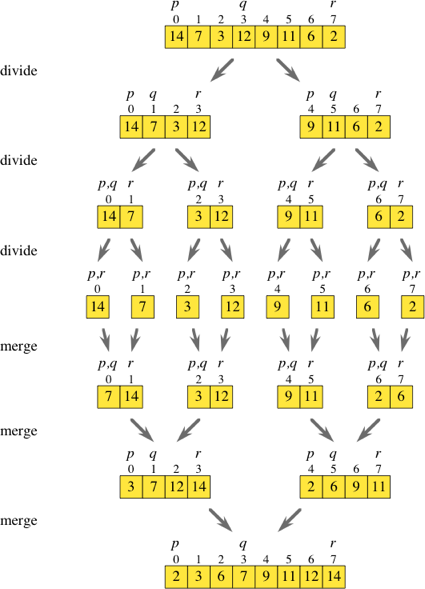
Zusammenführen, sortieren

Merge Sort ist also ein Divide-and-Conquer-Algorithmus. Während ich mir das obige Diagramm ansah, überlegte ich, ob es möglich wäre, im Grunde alle Teilungsschritte zu umgehen.

Wenn Sie beim Springen um zwei über das ursprüngliche Array iterieren, können Sie die Elemente am Index i und i + 1 abrufen und sie in ihre eigenen sortierten Arrays einfügen. Sobald Sie alle diese Sub-Arrays ([7,14], [3,12], [9,11] und [2,6], wie im Diagramm gezeigt) haben, können Sie einfach mit der normalen Zusammenführungsroutine fortfahren ein sortiertes Array.

Ist es weniger effizient, durch das Array zu iterieren und die erforderlichen Unterarrays sofort zu generieren, als die Divisionsschritte in ihrer Gesamtheit auszuführen?

— Jimmy_Rustle
quelle

Related: cs.stackexchange.com/questions/77075/…

— Omar

Antworten:

Die Verwirrung ergibt sich aus dem Unterschied zwischen der konzeptuellen Beschreibung des Algorithmus und seiner Implementierung .

Die logische Sortierung beim Zusammenführen wird als Aufteilen des Arrays in kleinere Arrays und anschließendes Zusammenführen dieser Arrays beschrieben. "Aufteilen des Arrays" bedeutet jedoch nicht "Erstellen eines völlig neuen Arrays im Speicher" oder ähnliches - es könnte in Code wie folgt implementiert werden

/*
 * Note: array is now split into  [0..n) and [n..N)
 */

dh es findet keine eigentliche Arbeit statt, und die "Aufteilung" ist rein konzeptionell. Also, was Sie vorschlagen, funktioniert auf jeden Fall, aber logischerweise "spalten" Sie die Arrays immer noch auf - Sie brauchen nur keine Arbeit vom Computer, um dies zu tun :-)

— psmears
quelle

Persönlich mag ich die Bottom-up-Merge-Sortierung sehr, da sie einfacher zu implementieren ist, sodass Sie die Zuweisung eines temporären Puffers auf jeder Rekursionsstufe vermeiden können. Stattdessen weisen Sie einen Puffer einmal und Ping-Pong zwischen ihnen.

— Ratschenfreak

Diese - Teilung ist rechnerisch ein No-Op ... Plus-OPs-Vorschlag ist nur eine Einführung eines Äquivalents zu einer Zusammenführung von Einzelelement-Arrays und die Verwendung der Zusammenführung ab dem 2. Schritt, was überflüssig erscheint, da die ursprüngliche Zusammenführung genauso gut funktioniert. Es macht keinen Sinn, das zu optimieren. Es werden nur redundante Konzepte und Logik eingeführt.

— Luk32

@ratchetfreak: Ich liebe es auch, aber leider ist es nicht gleichbedeutend mit top-down (zumindest die Version, die ich kenne). Das Zusammenführen wird anders ausgeführt, im Grunde wird auf die nächste Array-Länge mit Potenz 2 aufgerundet, was meiner Meinung nach sogar etwas langsamer sein könnte. Kennen Sie eine Bottom-Up-Version, bei der genau das gleiche zusammengeführt wird, ohne dass dafür an anderer Stelle hohe Kosten anfallen?

— user541686

@Mehrdad das einzige wirkliche Problem ist der kleine Schwanz, in dem zusammengeführt werden muss. Im schlimmsten Fall bedeutet dies, dass ein weiterer Durchgang in einem einzelnen Element für Arrays von Länge zusammengeführt werden muss 1<<n+1. Ich bin mir jedoch sicher, dass Sie die Einstellungen so anpassen können, dass ein zu kleiner Schwanz in einem niedrigeren Durchgang zusammengeführt wird.

— Ratschenfreak

@psmears "Sie brauchen nur keine Arbeit vom Computer, um dies zu tun" - ich vermute also, dass die Performancekosten von n Aufrufen einer rekursiven Divisionsfunktion (7 Aufrufe im Beispieldiagramm) im Grunde vernachlässigbar sind?

— Jimmy_Rustle

Ich denke, was Sie meinen, ist die Bottom-up-Implementierung . In der Bottom-Up-Implementierung beginnen Sie mit einzelnen Zellenelementen und bewegen sich nach oben, indem Sie Elemente in größeren sortierten Listen / Arrays zusammenführen. Kehren Sie einfach die Pfeile in der obigen Abbildung um und beginnen Sie beim mittleren Array, dh bei Arrays mit einem Element.

Möglicherweise möchten Sie auch die Zusammenführungssortierung optimieren, indem Sie die Arrays teilen, bis sie eine konstante Größe erreichen. Anschließend sortieren Sie sie einfach mit der Einfügesortierung.

Andernfalls ist das Sortieren ohne Aufteilung des Arrays nicht möglich. Tatsächlich besteht der Kern der Sortierung "Zusammenführen" darin, Unterfelder zu unterteilen und zu sortieren, dh zu teilen und zu erobern.

— fade2black
quelle