Schrittweise Erklärung der K-fachen Kreuzvalidierung mit Rastersuche zur Optimierung von Hyperparametern

Ich bin mir der Vorteile der k-fachen (und ausgelassenen) Kreuzvalidierung sowie der Vorteile der Aufteilung Ihres Trainingssatzes zur Erstellung eines dritten Holdout-Validierungssatzes bewusst, den Sie zur Bewertung verwenden Modellleistung basierend auf der Auswahl von Hyperparametern, sodass Sie diese optimieren und optimieren und die besten auswählen können, die schließlich am realen Testsatz bewertet werden sollen. Ich habe beide unabhängig voneinander in verschiedenen Datensätzen implementiert.

Ich bin mir jedoch nicht ganz sicher, wie ich diese beiden Prozesse integrieren soll. Ich bin mir sicher bewusst, dass dies möglich ist (verschachtelte Kreuzvalidierung, glaube ich?), Und ich habe Leute gesehen, die es erklärt haben, aber nie so detailliert, dass ich die Einzelheiten des Prozesses tatsächlich verstanden habe.

Es gibt Seiten mit interessanten Grafiken, die auf diesen Prozess verweisen (wie diesen ), ohne dass die genaue Ausführung der Teilungen und Schleifen klar ist. Hier ist der vierte eindeutig das, was ich tun möchte, aber der Prozess ist unklar:

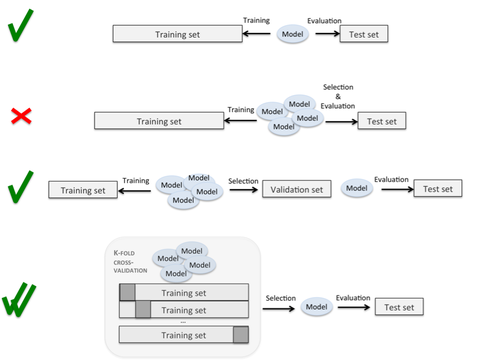
Es gibt frühere Fragen auf dieser Site, aber während diese die Bedeutung der Trennung von Validierungssätzen von Testsätzen beschreiben, gibt keiner von ihnen das genaue Verfahren an, mit dem dies durchgeführt werden soll.

Ist es so etwas wie: Behandeln Sie diese Falte für jede k-Falte als Testsatz, behandeln Sie eine andere Falte als Validierungssatz und trainieren Sie den Rest? Dies scheint so, als müssten Sie den gesamten Datensatz k * k-mal durchlaufen, damit jede Falte mindestens einmal als Training, Test und Validierung verwendet wird. Verschachtelte Kreuzvalidierung scheint zu implizieren, dass Sie eine Test- / Validierungsaufteilung in jeder Ihrer k-Falten durchführen, aber dies können sicherlich nicht genug Daten sein, um eine effektive Parametereinstellung zu ermöglichen, insbesondere wenn k hoch ist.

Könnte mir jemand helfen, indem er eine detaillierte Erklärung der Schleifen und Teilungen liefert, die eine k-fache Kreuzvalidierung ermöglichen (so dass Sie eventuell jeden Datenpunkt als Testfall behandeln können), während er gleichzeitig eine Parameteroptimierung durchführt (so dass Sie keine Vorangaben machen) Modellparameter und wählen Sie stattdessen diejenigen aus, die bei einem separaten Holdout-Set am besten funktionieren.

Hier ist die "standardmäßige" verschachtelte Kreuzvalidierungsprozedur zum Vergleichen zwischen einem festen Satz von Modellen (z. B. Rastersuche):

• Teilen Sie den Datensatz zufällig in Falten auf.$K$
• Für von 1 bis : $i$$K$
  • Lass testmich falten .$i$
  • Sei trainvalalle Daten außer denen, die in sind test.
  • Zufällig aufgeteilt trainvalin Unterfalten . Jede Unterfalte hat also einige Elemente aus der Außenfalte 1, einige aus der Außenfalte 2, ..., aber keine von ihnen hat welche aus der Außenfalte .$L$$(i, 1), (i, 2), \dots, (i, L)$$(i, j)$$i$
  • Für von 1 bis : $j$$L$
    • Sei valgefaltet .$(i, j)$
    • Sei trainalle Daten, die weder in noch testoder sind val.
    • Trainieren Sie jeden vorgeschlagenen Parametersatz trainund bewerten Sie ihn anhand valder Klassifizierungsgenauigkeit (RMSE), unabhängig davon, welches Kriterium Sie verwenden möchten.
  • Sehen Sie sich die durchschnittliche Punktzahl für jeden Parametersatz über die Falten an und wählen Sie die beste aus.$L$
  • Trainieren Sie ein Modell mit den besten Parametern trainval.
  • Bewerten Sie es auf testund speichern Sie die Genauigkeit / RMSE / was auch immer.
• Geben Sie den Mittelwert / Mittelwert + Standard / Boxplot / unabhängig von der Genauigkeit an.$K$

Der erste Schritt besteht darin, den gesamten Datensatz in Trainingssatz und Testsatz zu unterteilen. Und dann können Sie für das Trainingsset eine k-fache Kreuzvalidierung anwenden. Jedes Mal, wenn Sie das Modell mit k-1-Falte trainieren, verwenden Sie eine weitere Falte als Validierungssatz, um die Modellleistung zu bewerten. In diesem Schritt können Sie ein Modell mit der besten Leistung im Trainingssatz erhalten. Schließlich können Sie dieses Modell auf einen Testsatz anwenden, um die Leistung des im zweiten Schritt angepassten Modells zu bewerten. Hier ist ein Link, der hilfreich sein kann, um den Unterschied zwischen Validierungssatz und Testsatz zu verstehen. Was ist der Unterschied zwischen Testsatz und Validierungssatz?

In Übereinstimmung mit der Antwort von Dougal können Sie den Artikel von D. Krstajic et al. "Fallstricke bei der Kreuzvalidierung bei der Auswahl und Bewertung von Regressions- und Klassifizierungsmodellen", 2014 (doi: 10.1186 / 1758-2946-6-10 https://www.researchgate.net/publication/261217711_Cross-validation_pitfalls_when_selecting_and_assessing_regression_and_classification_models). Dort verwenden sie die verschachtelte Kreuzvalidierung für die Modellbewertung und die Kreuzvalidierung der Rastersuche, um die besten Merkmale und Hyperparameter auszuwählen, die im endgültig ausgewählten Modell verwendet werden sollen. Grundsätzlich präsentieren sie verschiedene Algorithmen zur Anwendung der Kreuzvalidierung mit Wiederholungen und unter Verwendung der verschachtelten Technik, die darauf abzielen, bessere Fehlerschätzungen bereitzustellen. Am Ende arbeiten sie die Experimente aus, die unter Verwendung der verschiedenen Algorithmen zur Modellbewertung und -auswahl durchgeführt wurden. Wie von den Autoren im Diskussionsteil des Artikels erwähnt: "Nach unserem Kenntnisstand ist die verschachtelte Kreuzvalidierung der beste nichtparametrische Ansatz für die Modellbewertung, wenn die Kreuzvalidierung für die Modellauswahl verwendet wird."