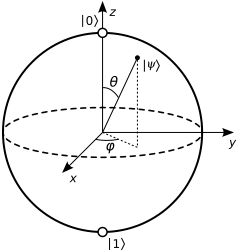
Wie denke ich über das Z-Tor in einer Bloch-Kugel nach?

10

Ich bin verwirrt darüber, wie man das $Z$ Tor in einer Bloch-Kugel versteht.

In Anbetracht der Matrix es verständlich, dass und . $Z = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}$ $Z|0\rangle = |0\rangle$ $Z|1\rangle = -|1\rangle$

Es wird hier erklärt , dass das Gatter eine Drehung um die Achse ist. Wie soll ich dann verstehen ? Da der Südpol ist, halte ich es für selbstverständlich, dass die Drehung um die Achse nichts bewirkt. $Z$ $\pi$ $Z$ $Z|1\rangle = -|1\rangle$ $|1\rangle$ $\pi$ $Z$

quantum-gate bloch-sphere

— Bick
quelle

7

Die Art und Weise, über die Bloch-Kugel nachzudenken, ist die Dichtematrix für den Zustand. wirkt entweder auf oder tut nichts, wie es für jede diagonale Dichtematrix gilt. Um den Effekt der Drehung zu sehen, müssen Sie untersuchen, wie eine nicht diagonale Dichtematrix durch geändert wird , z. B. . $Z$ $|0\rangle\langle 0|$ $|1\rangle\langle 1|$ $Z$ $|+\rangle\langle +|$

— DaftWullie
quelle

7

und auf den gleichen Punkt auf der BlochKugel zugeordnetda sie gleich sindbis zu globalen Phase. Algebraisch: wo bedeutet "gleich der globalen Phase up". Das heißt, es gibt einige so dass . $|1\rangle$ $-|1\rangle$ $|1\rangle \equiv -|1\rangle$ $\equiv$ $\theta$ $-|1\rangle = e^{i \theta} |1\rangle$

Was Sie verwirrt, ist, dass und , ist dies für lineare Kombinationen der beiden nicht wahr. Zum Beispiel Obwohl $|0\rangle \equiv Z |0\rangle$ $|1\rangle \equiv Z |1\rangle$ $Z |+\rangle \not\equiv Z |+\rangle$ . $|+\rangle = \frac{1}{\sqrt{2}}|0\rangle + \frac{1}{\sqrt{2}}|1\rangle$

— Craig Gidney
quelle

2

Laut Wikipedia können wir jeden reinen Zustand als schreiben

| ψ ⟩ = \cos (\frac{θ}{2}) | 0 ⟩ + e^{ich ϕ} Sünde (\frac{θ}{2}) | 1 ⟩

$|\psi\rangle = \cos\left( \frac{\theta}{2} \right) |0 \rangle + e^{i \phi} \sin\left( \frac{\theta}{2} \right) |1 \rangle$

Wobei und die Winkel auf der Blochkugel sind: $\theta$ $\phi$

Fast jeder Punkt auf der Oberfläche (dh der reine Zustand) hat eine eindeutige Darstellung in Bezug auf die Winkel, mit Ausnahme der Pole. Genau wie auf der Erde hat der Südpol keine genau definierte Länge (jede Länge funktioniert gleich) für die Zustand jeder Phase bedeutet dasselbe. Der "Breitengrad" ist hier , lassen Sie uns das in die Gleichung einfügen: $|1 \rangle$ $\phi$ $\theta$ $\pi$

| 1 ⟩ = \cos (\frac{π}{2}) | 0 ⟩ + e^{ich ϕ} Sünde (\frac{π}{2}) | 1 ⟩ =

$|1\rangle = \cos\left( \frac{\pi}{2} \right) |0 \rangle + e^{i \phi} \sin\left( \frac{\pi}{2} \right) |1 \rangle =$

= 0 + e^{ich ϕ} | 1 ⟩

$= 0 + e^{i \phi} |1 \rangle$

Wenn Sie mit Eulers Identität vertraut sind, werden Sie wahrscheinlich als Rotation in der komplexen Ebene erkennen. Insbesondere, da eine Rotation für , erhalten wir das berühmte , das schließlich zu gelangt . $e^{i \phi}$ $Z$ $\phi = \pi$ $e^{i \pi} = -1$ $|1 \rangle = - |1 \rangle$

— Norrius
quelle

1

Das ist falsch. Schreiben

ist irreführend: diese sind äquivalent Staaten, dass sie nur durch eine globale Phase unterscheiden, aber das bedeutet nicht , dass die Zustandsvektoren gleich sind. Sie erhalten dieses Ergebnis, weil Sie davon ausgehen, dass es eine Bijektion zwischen Zustandsvektoren und Punkten auf der Bloch-Kugel gibt, was nicht der Fall ist. Die Bijektion steht zwischen Punkten auf der Bloch-Kugel und Zuständen, die als Dichtematrizen beschrieben werden

| 1 ⟩ = - | 1 ⟩

$|1\rangle=-|1\rangle$

— glS

1 = - 1

$1=-1$

das ist dein anruf =). Ich denke, die richtige Antwort ist die von DaftWullie (ich glaube, der Fragesteller hatte ein ähnliches Missverständnis wie die in Ihrer Antwort). Ich sehe nicht mehr viel zu dieser Frage zu sagen

— glS