Dies ist eine Frage, zu der ich mich aufgrund dieser Frage inspiriert habe , in der festgestellt wird, dass Quantenglühen ein völlig anderes Berechnungsmodell ist als das übliche Schaltungsmodell. Ich habe das schon einmal gehört, und ich bin mir darüber im Klaren, dass das Gate-Modell nicht für das Quantenglühen gilt, aber ich habe nie ganz verstanden, warum das so ist oder wie man die Berechnungen analysiert, die ein Glühen kann. Wie ich aus mehreren Vorträgen (einige von D-Wave selbst!) Verstehe, spielt die Tatsache eine Rolle, dass die Annealer auf einen bestimmten Hamiltonianer beschränkt sind.
Warum kann Quantenglühen nicht durch ein Gate-Modell beschrieben werden?
Antworten:
Ein Quantum Glüht, wie eine D-Wave - Maschine ist eine physische Darstellung des Ising Modells und als solches hat ein 'Problem' Hamilton - Operator von der Form
Im Wesentlichen wird das zu lösende Problem auf den obigen Hamilton-Operator abgebildet. Das System startet mit der Hamilton - Operator und dem Glühparameter, s wird verwendet , um die Anfangshamiltonschen abzuzubilden H I auf das Problem Hamilton - Operator H P unter Verwendung von H ( s ) = ( 1 - s ) H I + s H P .
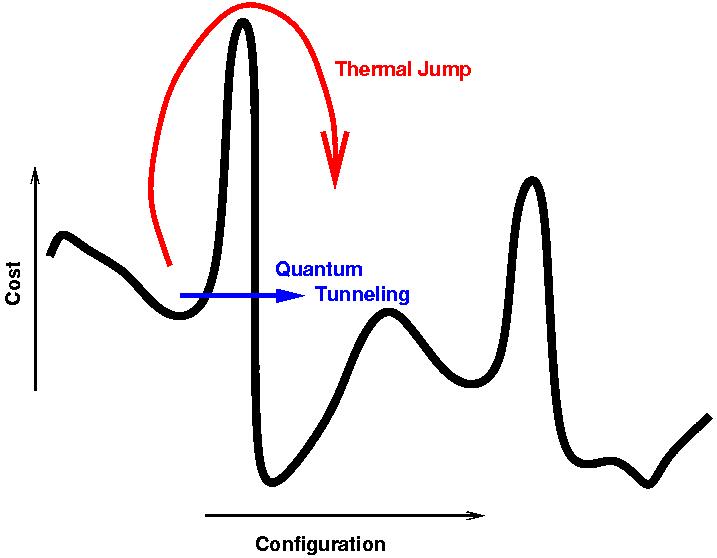
Da es sich um ein Tempern handelt, wird der Prozess langsam genug durchgeführt, um in der Nähe des Grundzustands des Systems zu bleiben, während der Hamilton-Wert dem des Problems angepasst wird. Dabei wird das Tunneln verwendet, um in der Nähe des Grundzustands zu bleiben, wie in der Antwort von Nat beschrieben .
Warum kann dies nicht zur Beschreibung eines Gate-Modells QC verwendet werden? Das obige ist ein quadratisches Problem der unbeschränkten binären Optimierung (QUBO) , das NP-schwer ist ... In der Tat ist hier ein Artikel, der eine Reihe von NP-Problemen auf das Ising-Modell abbildet . Jedes NP-Problem kann auf jedes NP-harte Problem in der Polynomzeit abgebildet werden, und die ganzzahlige Faktorisierung ist in der Tat ein NP-Problem.
Nun, die Temperatur ist ungleich Null, so dass sie während des gesamten Temperns nicht im Grundzustand sein wird, und als Ergebnis ist die Lösung immer noch nur eine ungefähre. Anders ausgedrückt ist die Wahrscheinlichkeit eines Misserfolgs größer als die Hälfte (es ist bei weitem nicht annähernd annehmbar, eine annehmbare Erfolgswahrscheinlichkeit zu haben, verglichen mit dem, was eine universelle Qualitätskontrolle als "annehmbar" ansieht) Die aktuelle Maschine liegt bei etwa und dies wird sich nur mit zunehmender Größe verschlechtern. Der Anneal-Algorithmus ist nicht fehlerbehaftet. Überhaupt. Daher gibt es keine Möglichkeit zu wissen, ob Sie mit etwas wie der Ganzzahlfaktorisierung die richtige Lösung haben oder nicht.
Was es (im Prinzip) tut, ist, sehr schnell dem genauen Ergebnis zu nahe zu kommen, aber dies hilft nichts, wenn das genaue Ergebnis erforderlich ist, da es immer noch äußerst schwierig ist, von "fast korrekt" zu "korrekt" zu wechseln ( dh vermutlich immer noch NP im Allgemeinen, wenn das ursprüngliche Problem in NP ist) Problem in diesem Fall, da die Parameter, die eine 'fast korrekte' Lösung ergeben, nicht notwendigerweise irgendwo in der Nähe der Parameter verteilt werden, die das / die ergeben richtige Lösung.
Zur Verdeutlichung: Was dies bedeutet, ist, dass ein Quantum Annealer (QA) immer noch exponentielle Zeit benötigt (wenn auch möglicherweise eine schnellere exponentielle Zeit), um NP-Probleme wie die ganzzahlige Faktorisierung zu lösen, wobei eine universelle QC eine exponentielle Beschleunigung ergibt und dieselbe lösen kann problem in poly zeit. Dies bedeutet, dass eine Qualitätssicherung eine universelle Qualitätskontrolle nicht in Poly-Zeit simulieren kann (andernfalls können Probleme in Poly-Zeit gelöst werden, die nicht möglich sind). Wie in den Kommentaren ausgeführt, bedeutet dies nicht , dass eine Qualitätssicherung bei anderen Problemen wie der Datenbanksuche nicht die gleiche Geschwindigkeit erzielen kann.
1
Wenn ich das richtig verstehe, sagen Sie im Grunde, dass ein Quanten-Annealer keinen Quanten-Schaltkreis beschreiben kann, weil das Problem, das Minimum eines beliebigen Hamilton-Operators zu finden, NP-schwer ist. Ich verstehe diese Implikation nicht. Die Simulation von Quantenschaltungen ist im Allgemeinen auch klassisch schwer zu simulieren (siehe z. B. 1610.01808 )
—
glS
Es ist auch bekannt, dass einige Probleme, die durch als Quantenschaltungen ausgedrückte Algorithmen lösbar sind, auch durch Quantenglühen lösbar sind. Ein bemerkenswertes Beispiel ist die Datenbanksuche (siehe z. B. Abschnitt II von 1006.1696 ). Dies bedeutet, dass man in gewissem Sinne unter bestimmten Umständen eine q-Schaltung auf ein q-Glühproblem abbilden kann . Macht dies nicht auch Ihren dritten Absatz ungültig (insbesondere die Behauptung, dass dies nicht zur Beschreibung eines Gate-Modells QC verwendet werden kann )
—
glS
@glS nein, überhaupt nicht - es dauert immer noch exponentiell lange, um die Minute (gemäß dem Artikel in Ihrem zweiten Kommentar) eines NP-harten Problems zu finden. Es gibt also Probleme in P (z. B. Datenbanksuche), bei denen die Beschleunigung auftreten kann Um ein NP-Problem zu lösen, ist exponentiell viel Zeit erforderlich, um innerhalb eines begrenzten Fehlers zu liegen. Eine universelle Qualitätskontrolle kann möglicherweise dasselbe Problem in der Polyzeit lösen, z. B. die Ganzzahlfaktorisierung. Da QA dies nicht kann, kann eine QA keine universelle QC in
—
Polyzeit
Ok, aber das ist nicht das, was Sie in der Antwort sagen (oder zumindest nicht explizit). Aus der Antwort geht hervor, dass Sie sagen, dass QA niemals zur Lösung eines Problems verwendet werden kann, das über das Gate-Modell QC gelöst wurde. Das ist etwas ganz anderes als zu sagen, dass die Qualitätssicherung ein NP-hartes Problem nicht effizient lösen kann (was manchmal durch eine Quantenschaltung gelöst werden könnte ... obwohl ich dies nicht für erwiesen halte, da wir nicht wissen, ob Factoring wirklich ist NP-harte und die meisten anderen Probleme, bei denen ein Quantenvorteil nachgewiesen wurde, sind meines Wissens keine Entscheidungsprobleme.
—
glS
Ich habe eine Bearbeitung vorgenommen, die hoffentlich die Dinge klarer macht. Es ist nicht bekannt, ob P = NP ist oder nicht, aber es ist nach heutigem Kenntnisstand immer noch ein konkretes Beispiel für eine exponentiell schnellere
—
Qualitätskontrolle
Das Tempern ist eher eine analoge Taktik.
Das Wesentliche ist, dass Sie eine seltsame Funktion haben, die Sie optimieren möchten. Also hüpfen Sie herum. Die " Temperatur " ist anfangs sehr hoch, so dass der ausgewählte Punkt stark springen kann. Dann, wenn der Algorithmus " abkühlt ", sinkt die Temperatur und das Prellen wird weniger aggressiv.
Letztendlich handelt es sich um ein lokales Optima, das im Idealfall dem globalen Optima entspricht.
Hier ist eine Animation zum simulierten Tempern (nicht quantum):
Aber es ist so ziemlich das gleiche Konzept für das Quantenglühen :
Im Gegensatz dazu ist Gate-Logik weitaus digitaler als analog. Es geht eher um Qubits und logische Operationen als nur darum, nach einem chaotischen Auf und Ab ein Ergebnis zu finden.
Danke, das klärt für mich gewisse Einschränkungen. Kennen Sie irgendwelche Probleme, die nicht als Glühproblem umformuliert werden können? (Ich weiß, dass Wikipedia angegeben hat, dass Shors Algorithmus nicht möglich war, weil es sich um ein "Hill Climbing" -Problem handelt würde sie gerne hören :)
—
Emily Tyhurst
@EmilyTyhurst Technisch lässt sich jedes Problem im Bergsteigen beschreiben. Es ist auch eine Frage, wie gut sich das Problem verhält, wenn es im Bergsteigerformat beschrieben wird. Probleme, die nicht gut passen, können unglaublich hässlich sein. Bei völlig nicht konvexen Problemen wäre Bergsteigen bestenfalls eine Brute-Force-Suche.
—
Nat
@EmilyTyhurst Hah, lese deinen Kommentar falsch in die entgegengesetzte Richtung. xD Aber ja, Sie können simuliertes Tempern auf einem Quantencomputer genauso durchführen wie auf einem klassischen Computer. Dann, nehme ich an, wird es mehr eine Frage der Semantik , ob wir es " Quantenglühen " nennen oder nicht .
—
Nat
@EmilyTyhurst Ja, sie sind definitiv alle untereinander konvertierbar. Ich meine, es ist ein bisschen wie das Konzept der Turing-Vollständigkeit - wenn wir irgendeine Art von vollständiger Logik haben, können wir fast alles andere damit konstruieren.
—
Nat
Ein wichtiger Punkt des Quantenglühens ist das adiabatische Ändern des Hamiltonian, so dass der Zustand jederzeit ein Grundzustand des (sich ändernden) Hamiltonian bleibt, und Sie erhalten den gs des endgültigen Hamiltonian, der das Ziel des Protokolls ist . Wie hängt das mit dem "Springen" zusammen, das Sie hier beschreiben? Dieser Artikel ( 1006.1696 ) kann diesbezüglich von Interesse sein (insbesondere der letzte Teil der zweiten Spalte der ersten Seite).
—
glS