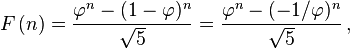Testen Sie, ob eine Zahl Fibonacci ist

Ich weiß, wie man die Liste der Fibonacci-Zahlen erstellt, aber ich weiß nicht, wie ich testen kann, ob eine bestimmte Zahl zur Fibonacci-Liste gehört - eine Möglichkeit, die mir in den Sinn kommt, besteht darin, die Liste der Fibonacci-Zahlen zu erstellen. Zahlen bis zu dieser Zahl und sehen, ob es zum Array gehört, aber es muss eine andere, einfachere und schnellere Methode geben.

Irgendwelche Ideen ?

Ein sehr schöner Test ist, dass N genau dann eine Fibonacci-Zahl ist, wenn 5 N^2 + 4oder 5N^2 – 4eine quadratische Zahl ist. Ideen, wie Sie effizient testen können, ob eine Zahl quadratisch ist, finden Sie in der SO-Diskussion .

Hoffe das hilft

Eine positive ganze Zahl ω ist genau dann eine Fibonacci-Zahl, wenn entweder 5ω ² + 4 oder 5ω ² - 4 ein perfektes Quadrat ist.

Weitere Informationen finden Sie unter Die fabelhaften Fibonacci-Zahlen .

Während mehrere Personen auf die Lösung mit dem perfekten Quadrat hinweisen, wird eine Fibonacci-Zahl quadriert, was häufig zu einem massiven Produkt führt.

Es gibt weniger als 80 Fibonacci-Zahlen, die sogar in einer Standard-64-Bit-Ganzzahl gespeichert werden können.

Hier ist meine Lösung, die völlig kleiner arbeitet als die zu testende Anzahl.
(In C # geschrieben, mit Basistypen wie doubleund long. Der Algorithmus sollte jedoch für größere Typen gut funktionieren.)

static bool IsFib(long T, out long idx)
{
    double root5 = Math.Sqrt(5);
    double phi = (1 + root5) / 2;

    idx    = (long)Math.Floor( Math.Log(T*root5) / Math.Log(phi) + 0.5 );
    long u = (long)Math.Floor( Math.Pow(phi, idx)/root5 + 0.5);

    return (u == T);
}

Parameter 2 ist der "Index" in der Fibonacci-Sequenz.
Wenn der zu testende Wert Teine Fibonacci-Zahl ist, ist idxdies der 1-basierte Index dieser Zahl in der Fibonacci-Sequenz. (mit einer bemerkenswerten Ausnahme)

Die Fibonacci-Sequenz ist 1 1 2 3 5 8 13usw.
3 ist die 4. Zahl in der Sequenz: IsFib(3, out idx);wird zurückgegeben trueund bewertet 4.
8 ist die 6. Zahl in der Sequenz: IsFib(8, out idx);wird zurückgegeben trueund bewertet 6.
13 ist die 7. Zahl; IsFib(13, out idx);wird zurückkehren trueund Wert 7.

Die einzige Ausnahme ist IsFib(1, out idx);, dass zurückgegeben wird 2, obwohl der Wert 1 sowohl bei Index 1 als auch bei Index 2 angezeigt wird.

Wenn IsFibeine Nicht-Fibonacci-Zahl übergeben wird, wird diese zurückgegeben false, und der Wert von idxist der Index der größten Fibonacci-Zahl kleiner als T.

16 ist kein Fibonacci-Wert.
IsFib(16, out idx);wird zurückkehren falseund Wert 7.
Sie können die Binet-Formel verwenden , um den Index 7 in den Fibonacci-Wert 13 umzuwandeln. Dies ist die größte Zahl unter 16.

#!/bin/bash
victim="144"
curl http://aux.planetmath.org/files/objects/7680/fib.txt | sed 's/^[0-9]*//;s/[ \t]//g' | grep "^$victim$" >/dev/null 2>/dev/null
if [[ $? -eq 0 ]] ; then
    echo "$victim is a fibonacci number"
else
    echo "$victim aint"
fi

Wenn Ihre Zahlen eine begrenzte Größe haben, reicht es aus, einfach alle Fibonacci-Zahlen unterhalb der Obergrenze in eine Hashtabelle zu setzen und das Containment zu testen. Es gibt nur sehr wenige Fibonacci-Zahlen (zum Beispiel nur 38 unter 5 ml), da sie exponentiell wachsen.

Wenn Ihre Zahlen keine begrenzte Größe haben, ist der vorgeschlagene Trick mit quadratischen Tests mit ziemlicher Sicherheit langsamer als das Erzeugen der Fibonacci-Sequenz, bis die Zahl gefunden oder überschritten wird.

Schauen Sie sich Binets Formel an, um eine Lösung zu finden.
(Suchen Sie nach "Closed-Form Expression" unter Fibonacci Number auf Wikipedia)

Es heißt, dass die Folge der Fibonacci-Zahlen durch eine einfache geschlossene Formel erzeugt wird:

Ich glaube, wenn Sie nach einer Ganzzahl suchen nund testen, ob sie neine ganze Zahl ist, haben Sie Ihre Antwort.

Bearbeiten Wie @psmears hervorhebt, enthält derselbe Wikipedia-Artikel auch einen Abschnitt zum Erkennen von Fibonacci-Zahlen. Wikipedia ist eine ausgezeichnete Quelle.

Die positive ganze Zahl ω ist eine Fibonacci-Zahl

Genau dann, wenn eines von 5ω ² + 4 und 5ω ² - 4 ein perfektes Quadrat ist

aus den (fabelhaften) FIBONACCI-Zahlen von Alfred Posamentier und Ingmar Lehmann

bool isFibonacci(int  w)
{
       double X1 = 5 * Math.Pow(w, 2) + 4;
       double X2 = 5 * Math.Pow(w, 2) - 4;

       long X1_sqrt = (long)Math.Sqrt(X1);
       long X2_sqrt = (long)Math.Sqrt(X2);   

       return (X1_sqrt*X1_sqrt == X1) || (X2_sqrt*X2_sqrt == X2) ;
}

Ich habe es aus dieser Quelle kopiert

Snippet, das Fibonacci-Zahlen zwischen 1kund druckt 10k.

for (int i = 1000; i < 10000; i++)
{
         if (isFibonacci(i))
              Console.Write(" "+i);
}

OMG Es gibt nur VIER !!!

Mit anderer Methode

from math import *

phi = 1.61803399
sqrt5 = sqrt(5)

def F(n):
    return int((phi**n - (1-phi)**n) /sqrt5)

def isFibonacci(z):
    return F(int(floor(log(sqrt5*z,phi)+0.5))) == z

print [i for i in range(1000,10000) if isFibonacci(i)]

Siehe den Abschnitt "Erkennen von Fibonacci-Zahlen" im Wikipedia-Artikel über die Fibonacci-Zahlen .

Da die Fibonacci-Zahlen exponentiell wachsen, ist die von Ihnen vorgeschlagene Methode ziemlich schnell. Ein anderer ist dies .

Basierend auf früheren Antworten von mir und psmears habe ich diesen C # -Code geschrieben.

Es geht die Schritte langsam durch und kann deutlich reduziert und optimiert werden:

// Input: T: number to test.
// Output: idx: index of the number in the Fibonacci sequence.
//    eg: idx for 8 is 6. (0, 1, 1, 2, 3, 5, 8)
// Return value: True if Fibonacci, False otherwise.
static bool IsFib(long T, out int idx)
{
    double root5 = Math.Sqrt(5);
    double PSI = (1 + root5) / 2;

    // For reference, IsFib(72723460248141) should show it is the 68th Fibonacci number

    double a;

    a = T*root5;
    a = Math.Log(a) / Math.Log(PSI);
    a += 0.5;
    a = Math.Floor(a);
    idx = (Int32)a;

    long u = (long)Math.Floor(Math.Pow(PSI, a)/root5 + 0.5);

    if (u == T)
    {
        return true;
    }
    else
    {
        idx = 0;
        return false;
    }
}

Tests haben ergeben, dass dies für die ersten 69 Fibonacci-Zahlen funktioniert, für die 70er jedoch nicht funktioniert.

F(69) = 117,669,030,460,994 - Works
F(70) = 190,392,490,709,135 - Fails

Wenn Sie keine BigInt-Bibliothek verwenden, ist es wahrscheinlich besser, eine einfache Nachschlagetabelle der Fibonacci-Zahlen zu haben und dies zu überprüfen, als einen Algorithmus auszuführen.

Eine Liste der ersten 300 Nummern ist online verfügbar.

Dieser Code beschreibt jedoch einen funktionsfähigen Algorithmus, vorausgesetzt, Sie verfügen über ausreichende Genauigkeit und überlaufen Ihr Zahlendarstellungssystem nicht.

Aus Wikipedia: http://en.wikipedia.org/wiki/Fibonacci_number

Eine positive ganze Zahl z ist genau dann eine Fibonacci-Zahl, wenn eine von 5z ^ 2 + 4 oder 5z ^ 2 - 4 ein perfektes Quadrat ist.

Betreff: Ahmads Code - ein einfacherer Ansatz ohne Rekursion oder Zeiger, ziemlich naiv, erfordert jedoch so gut wie keine Rechenleistung für etwas anderes als wirklich titanische Zahlen (ungefähr 2N Additionen zur Überprüfung der N-ten Fib-Zahl, was auf einer modernen Maschine Millisekunden dauern wird schlimmstenfalls)

// gibt pos zurück, wenn es etwas findet, 0, wenn es nichts findet (C / C ++ behandelt jeden Wert! = 0 als wahr, also dasselbe Endergebnis)

int isFib (long n)
{
    int pos = 2;
    long last = 1;
    long current = 1;
    long temp;

    while (current < n)
    {
        temp = last;
        last = current;
        current = current + temp;
        pos++;
    }

    if (current == n)
        return pos;
    else
        return 0;

}

Der allgemeine Ausdruck für eine Fibonacci-Zahl ist F (n) = [[(1 + sqrt (5)) / 2] sup n + 1 - [(1-sqrt (5)) / 2] sup n + 1] / sqrt (5) ..... (*) Das zweite Exponential geht für großes n auf Null und führt die numerischen Operationen aus, die wir erhalten. F (n) = [(1.618) sup n + 1] / 2.236

Wenn K die zu testende Zahl ist, sollte log (k * 2.2336) / log (1.618) eine ganze Zahl sein!

Beispiel für K gleich 13 mein Rechner gibt die Antwort 7.00246 Für K gleich 14 ist die Antwort 7.1564.

Sie können das Vertrauen in das Ergebnis erhöhen, indem Sie die der Antwort am nächsten liegende Ganzzahl verwenden und (*) einsetzen, um zu bestätigen, dass das Ergebnis K ist

Wie groß sind die Zahlen, mit denen Sie es zu tun haben?

Könnte eine Nachschlagetabelle für Sie funktionieren? (eine vorberechnete Liste von Zahlen, in denen Sie suchen können)

Es gibt auch einen Ausdruck in geschlossener Form , den Sie wahrscheinlich umkehren könnten, um die Antwort analytisch zu erhalten (obwohl ich kein Mathematiker bin, kann ich nicht versprechen, dass dieser Vorschlag Sinn macht).

Ich habe einige Benchmarks für die hier vorgestellten Methoden durchgeführt, zusammen mit der einfachen Addition, der Vorberechnung eines Arrays und dem Speichern der Ergebnisse in einem Hash. Zumindest für Perl ist die Quadrierungsmethode etwas schneller als die logarithmische Methode, vielleicht 20% schneller. Wie abelenky betont, ist es ein Kompromiss zwischen der Frage, ob Sie den Raum zum Quadrieren von Bitzahlen haben.

Der schnellste Weg ist sicherlich, alle Fibonacci-Nummern in Ihrem Domain-Bereich zu hashen. In Anlehnung an einen anderen Punkt, den abelenky hervorhebt, gibt es nur 94 dieser Saugnäpfe, die weniger als 2 ^ 64 sind.

Sie sollten sie einfach vorberechnen und in einen Perl-Hash, ein Python-Wörterbuch oder was auch immer einfügen.

Die Eigenschaften von Fibonacci-Zahlen sind sehr interessant, aber wenn Sie sie verwenden, um zu bestimmen, ob eine Ganzzahl in einem Computerprogramm eine solche ist, schreiben Sie bei jedem Programmstart eine Unterroutine, um pi zu berechnen.

Dies ist meine Lösung. Ich bin mir nicht sicher, ob es Benchmarks gibt. Ich hoffe das hilft!

def is_fibonacci?(i)
  a,b=0,1
    until b >= i
        a,b=b,a+b
        return true if b == i
    end
end

was a, b = b, a + b tut

 0, 1 = 1, 0 +1
 1, 1 = 1, 1 + 1
 1, 2 = 2, 1 + 2
 2, 3 = 3, 2 + 3

fib1 = fib2
fib2 = fib1 + fib2

Eine Scala-Version-

def isFib(n: Int): Boolean = {

def checkFib(f1: Int = 1, f2: Int = 1): Boolean = {

if(n == f1 || n == f2) true
else if(n < f2) false
else checkFib(f2, f1+f2)

}

checkFib()

}

Die Java-Lösung kann wie folgt ausgeführt werden. Trotzdem kann es optimiert werden

Die folgende Lösung funktioniert für

1. 1 ≤ T ≤ 10 ^ 5
2. 1 ≤ N ≤ 10 ^ 10

T ist die Anzahl der Testfälle, N ist der Zahlenbereich

    import java.util.Scanner;
    import java.math.BigDecimal;
    import java.math.RoundingMode;

    public class FibonacciTester {
        private static BigDecimal zero = BigDecimal.valueOf(0);
        private static BigDecimal one = BigDecimal.valueOf(1);
        private static BigDecimal two = BigDecimal.valueOf(2);
        private static BigDecimal four = BigDecimal.valueOf(4);
        private static BigDecimal five = BigDecimal.valueOf(5);

        public static void main(String[] args) {
            Scanner sc = new Scanner(System.in);
            int n = sc.nextInt();
            BigDecimal[] inputs = new BigDecimal[n];
            for (int i = 0; i < n; i++) {
                inputs[i] = sc.nextBigDecimal();
            }

            for (int i = 0; i < inputs.length; i++) {
                if (isFibonacci(inputs[i]))
                    System.out.println("IsFibo");
                else
                    System.out.println("IsNotFibo");
            }


        }

        public static boolean isFibonacci(BigDecimal num) {
            if (num.compareTo(zero) <= 0) {
                return false;
            }

            BigDecimal base = num.multiply(num).multiply(five);
            BigDecimal possibility1 = base.add(four);
            BigDecimal possibility2 = base.subtract(four);


            return (isPerfectSquare(possibility1) || isPerfectSquare(possibility2));
        }

        public static boolean isPerfectSquare(BigDecimal num) {
            BigDecimal squareRoot = one;
            BigDecimal square = one;
            BigDecimal i = one;
            BigDecimal newSquareRoot;
            int comparison = -1;

            while (comparison != 0) {
                if (comparison < 0) {
                    i = i.multiply(two);
                    newSquareRoot = squareRoot.add(i).setScale(0, RoundingMode.HALF_UP);
                } else {
                    i = i.divide(two);
                    newSquareRoot = squareRoot.subtract(i).setScale(0, RoundingMode.HALF_UP);
                }

                if (newSquareRoot.compareTo(squareRoot) == 0) {
                    return false;
                }

                squareRoot = newSquareRoot;
                square = squareRoot.multiply(squareRoot);
                comparison = square.compareTo(num);
            }

            return true;
        }
    }

int isfib(int n /* number */, int &pos /* position */)
{
   if (n == 1)
   {
      pos=2;  // 1 1
      return 1;
   }
   else if (n == 2)
   {
      pos=3;  // 1 1 2
      return 1;
   }
   else
   {
      int m = n /2;
      int p, q, x, y;
      int t1=0, t2 =0;
      for (int i = m; i < n; i++)
      {
        p = i;
        q = n -p;    // p + q = n
        t1 = isfib(p, x);
        if (t1) t2 = isfib(q, y);
        if (t1 && t2 && x == y +1)
        {
           pos = x+1;
           return 1; //true
        }
      }
      pos = -1;
      return 0; //false
   }
}

Wie wäre es damit?

#include <stdio.h>
#include <math.h>

int main()
{
int number_entered, x, y;

printf("Please enter a number.\n");
scanf("%d", &number_entered);
x = y = 5 * number_entered^2 + 4;        /*Test if 5N^2 + 4 is a square number.*/
x = sqrt(x);
x = x^2;
if (x == y)
{
        printf("That number is in the Fibonacci sequence.\n");
    }
x = y = 5 * number_entered^2 - 4;        /*Test if 5N^2 - 4 is a square number.*/
x = sqrt(x);
x = x^2;
if (x == y)
{
    printf("That number is in the Fibonacci sequence.\n");
}
else
{
    printf("That number isn't in the Fibonacci sequence.\n");
}
return 0;
}

Ob das funktioniert?