Warum stimmt die Fokusentfernung, bei der mein Objektiv die Vergrößerung 1 hat, nicht mit der Formel überein?

Auf der Vergrößerungs- Wikipedia-Seite habe ich folgende Gleichheit:

M = d _i / d _o = f / (d _o - f) = (d _i - f) / f

mit M die Vergrößerung, f die Brennweite, d _o die Entfernung vom Objekt zum Objektiv und d _i die Entfernung vom Objektiv zum Sensor.

Wenn also die Vergrößerung 1 ist, sollten wir d _i = d _o = 2f haben.

Bei meinem Makroobjektiv (EF 100 mm 1: 2,8 L IS USM-Makro) beträgt der Mindestarbeitsabstand (vom Motiv zum Sensor) 30 cm, bei diesem Abstand beträgt die Vergrößerung 1. Nach dem, was ich aus der Formel nicht verstehe, sollte dieser Abstand d sein _i + _do = 4f = 40 cm.

Ich glaube, ich vermisse etwas. Kann jemand erklären, wo ich falsch liege?

Die Gleichung geht von einer einfachen Einzelelementlinse aus, die bilateral symmetrisch ist. Das Kameraobjektiv wird zur Minderung der 7 Hauptaberrationen (Mängel, die sich verschlechtern) unter Verwendung mehrerer einzelner Glaslinsenelemente konstruiert. Einige haben eine positive Leistung, andere eine negative. Einige haben einen Luftabstand, andere sind miteinander verklebt. Da dieses Array ziemlich komplex wird, wird der Punkt, von dem aus wir die Brennweite messen, wahrscheinlich vom physischen Zentrum des Objektivtubus weg verschoben.

Bei einem echten Tele-Design wird der hintere Knoten (Messpunkt) nach vorne verschoben. Diese Aktion verkürzt die Länge des Objektivtubus und macht das Halten, Verwenden und Aufbewahren der Kamera und des Objektivs weniger umständlich. Bei einigen Konstruktionen kann der hintere Knoten tatsächlich vor dem Objektivtubus in die Luft fallen.

Wie die Gleichung besagt: Bei Einheit (Vergrößerung 1) beträgt die Objektentfernung 2 Brennweiten vorwärts und der Rückfokus 2 Brennweiten hinter dem hinteren Knoten. Das Problem ist --- Sie können den hinteren Knoten nicht leicht finden. Sobald jedoch die Vergrößerung 1 erreicht wurde, können Sie jetzt den Abstand zwischen Motiv und Bild messen. Viele Kameras bieten ein Symbol (mit einer Linie halbierter Kreis) auf dem Kamerarahmen. um die Position der Bildebene zu lokalisieren.

In jedem Fall die Entfernung zwischen Bild und Bild messen und durch 4 teilen. Diese Unterteilung zeigt die Brennweite. Teilen Sie durch 2 und diese Division lokalisiert den hinteren Knotenpunkt. Jetzt sind Sie besser gerüstet, um die „Formel des Linsenherstellers“ zu verwenden.

Zunächst ein großes Lob für Ihre Bemühungen, ein Fotografieproblem auf die ersten Prinzipien zu reduzieren.

Die beobachtete Diskrepanz beruht auf einer häufigen Vereinfachung. Ihr 100-mm-Objektiv wird von Optikingenieuren als "Linsenbaugruppe" bezeichnet. Wie Sie wahrscheinlich wissen, besteht es aus mehreren Linsenelementen in Gruppen , die zusammenarbeiten, um das von Ihrem Bildsensor gesehene Bild zu formen, zu verfeinern und zu übertragen.

Wenn Ihre 100-mm-Linsenbaugruppe aus einem einzelnen 100-mm-Linsenelement bestehen würde, würden Sie massive Verzerrungen aufweisen und nur Rot, Grün oder Blau könnten gleichzeitig scharfgestellt sein, aber die von Ihnen verknüpfte Gleichung für die Vergrößerung dünner Linsen würde zutreffen. Eine Vergrößerung von 1 würde erreicht, wenn das Objekt 200 mm vom Knotenpunkt entfernt ist und die Linsenanordnung physikalisch länger als 200 mm sein müsste. Selbst dann wäre dies nur streng genau in dem Maße , die die dünne Linse Gleichung geeignet ist (und es ist nicht besonders hier aneignen.) Eine richtige Antwort würde aus einer Ableitung der Gleichung des lensmaker

Eine Folge des Unterschieds zwischen einer Baugruppe und einer dünnen Linse sind bilokalisierte Knotenpunkte. Eine dünne Linse hat eine einzige Position sowohl für den vorderen als auch für den hinteren Knotenpunkt. Beide sind mit der Eintrittspupille zusammengeschlossen. Wenn dies für Ihre Linsenbaugruppe zutreffen würde, könnten Sie die Linse frei machendurch Drehung um die Blende Ihres Objektivs ohne Parallaxe zum Motiv oder Sensor. Ich bin sicher, wenn Sie dies mit dem 100-mm-Makro versuchen würden, würden Sie feststellen, dass es nicht wahr ist. Eine dicke Linse hat zwei Knotenpunkte, die nur dann zusammengeführt werden, wenn ihr Nettoindex 0 ist, dh sie hat keine Brennweite. Eine Linsenanordnung kann durch eine virtuelle dicke Linse mit zwei idealisierten Indizes angenähert werden, so dass die virtuelle Linse die gleichen Eckpunkte, relativen Brennweiten, Eintrittspupillen und (hervorstechenden) Knotenpunkte wie die Linsenanordnung aufweist.

Für zusätzliche Gutschrift können Sie die Beschreibung eines zusammengesetzten Objektivs überprüfen und versuchen, zu erraten, welche Kombinationen von Objektivbrennweiten die von Ihnen beschriebene Situation erzeugen würden. NB die "Teleskopvergrößerung". Dies ist im Wesentlichen das, was ein Objektivdesigner tut.

Weitere Informationen finden Sie in den verschiedenen Arten von Fotoobjektivdesigns

Die meisten Objektive mit fester Brennweite fokussieren durch Ändern ihrer Brennweite zusätzlich zum Verschieben der Knotenpunkte des Objektivs. Um auf ein Objekt in der Nähe der Kamera zu fokussieren, reduziert das Objektiv seine Brennweite. Eine als "100 mm" angegebene Linse ist normalerweise "100 mm, wenn sie auf unendlich fokussiert ist", aber nicht unbedingt, wenn sie auf ein nahes Objekt fokussiert ist.

Es gibt zwei Gründe, warum der Abstand zwischen Motiv und Bild bei Vergrößerung der Einheit nicht 40 cm beträgt:

1. Die Brennweite des Objektivs darf nicht 100 mm betragen
2. Der Abstand zwischen den Hauptebenen darf nicht Null sein.

Welcher dieser Gründe der wichtigste ist, lässt sich ohne detaillierte Informationen zum optischen Design der Linse nicht sagen.

Brennweite

Der auf dem Objektiv selbst angegebene Wert „100 mm“ ist eine nominelle Brennweite, die normalerweise ein gerundeter Wert der tatsächlichen Brennweite ist, wenn das Objektiv auf unendlich fokussiert ist.

Einige Objektive, die üblicherweise als "Einheitsfokussierungslinsen" bezeichnet werden, erzielen den Fokus, indem sie die optische Baugruppe als Ganzes bewegen. Diese Objektive haben eine Brennweite, die sich nicht mit der Fokussierung ändert. Viele komplexe Objektive, einschließlich praktisch aller modernen Makroobjektive, verfügen jedoch über eine Art „Nahbereichskorrektur“ (im Nikon-Sprachgebrauch): Ihre optische Formel ändert sich beim Fokussieren, wodurch Aberrationen besser korrigiert werden können. Diese Objektive haben eine Brennweite, die sich je nach Fokus ändert.

Diese beiden Tatsachen: Die Rundung der nominalen Brennweite und die Tatsache, dass sie beim Fokussieren variiert, bedeuten, dass Sie nicht wissen, wie hoch die tatsächliche Brennweite des Objektivs bei Einheitsvergrößerung ist.

Hauptflugzeuge

Die von Ihnen zitierte Wikipedia-Seite definiert d _o und d _i als den Abstand von der Linse zum Objekt (bzw. Bild). Beachten Sie jedoch, dass diese Definitionen in einem Abschnitt erscheinen, der sich speziell mit dünnen Linsen befasst . Da es sich bei Ihrer Linse um eine dicke Verbundlinse handelt, stellt sich die Frage nach der Anwendbarkeit der Formel.

Es stellt sich heraus, dass die Näherung der dünnen Linse in dieser Situation nicht anwendbar ist. Allerdings ist die Formel noch gültig in Zusammenhang mit dem , wenn interpretiert dicken Linse Modell. In diesem Modell wird die Ebene der dünnen Linse durch zwei Ebenen ersetzt, die als "Hauptebenen" bezeichnet werden:

• Die Hauptebene „vorne“ (oder „primär“ oder „objektseitig“) wird zum Messen von Entfernungen im Objektraum verwendet
• Die Hauptebene "Zurück" (oder "Sekundär" oder "Bildseite") wird zum Messen von Entfernungen im Bildraum verwendet

Dies sind konjugierte Ebenen mit Einheitsvergrößerung. In der folgenden Abbildung ( Quelle ) sind dies die vertikalen Ebenen, die durch H ₁ , N ₁ und H ₂ , N _{2 verlaufen} :

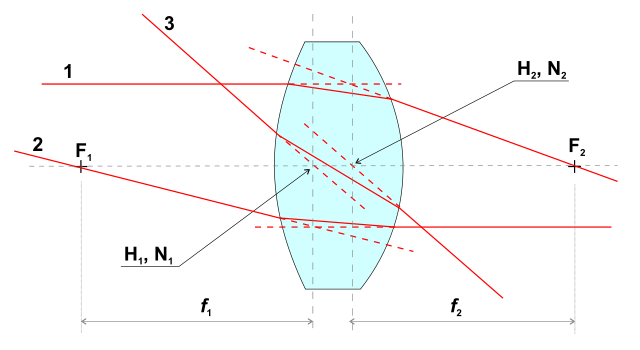
Es ist zu beachten, dass diese Art der Beschreibung eines optischen Systems in Bezug auf seine Kardinalpunkte (F _i , H _i und N _i oben) auch auf zusammengesetzte Linsen anwendbar ist. Siehe zum Beispiel diese alte Zeichnung eines Teleobjektivs ( Quelle ), bei der sich beide Hauptebenen (die vertikalen Ebenen durch N _i und N _o ) auf der linken Seite des Elements ganz links befinden:

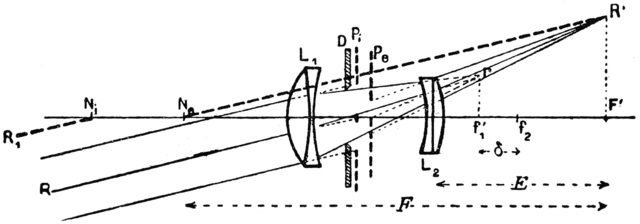
Somit ist Ihre Formel weiterhin gültig, sofern Sie Folgendes definieren:

• d _o als Abstand vom Subjekt zur primären Hauptebene
• d _i als Abstand von der sekundären Hauptebene zum Bild

Dies gibt den Abstand zwischen Motiv und Bild als an

d _o + e + d _i = 4f + e

bei Einheitsvergrößerung, wobei e der (möglicherweise negative) Abstand zwischen den Hauptebenen ist. Beachten Sie, dass die Näherung der dünnen Linse im Wesentlichen besagt, dass die Hauptebenen zusammenfallen (e = 0), aber für Ihren Fall nicht anwendbar ist.

Weitere Informationen zu diesem Thema finden Sie unter:

• Dieses kurze Video über Hauptflugzeuge
• diese Vorlesungsunterlagen zu dicken Linsen

Das Missverständnis der dünnen Linse

Ich habe diese Antwort hauptsächlich geschrieben, um ein weit verbreitetes Missverständnis zu beseitigen, das in einigen der Antworten hier auftaucht, einschließlich der von Ihnen akzeptierten: Ein fotografisches Objektiv entspricht einem dünnen Objektiv.

Es stellt sich heraus, dass in den meisten fotografischen Situationen (im Grunde genommen in allen Nicht-Makrosituationen) der Abstand zwischen Objekt und Objektiv viel größer ist als jeder charakteristische Abstand des Objektivs selbst. In solchen Situationen spielt es keine Rolle, welchen Referenzpunkt Sie zum Messen der Entfernung zum Motiv verwenden. Es ist dann zweckmäßig, den Abstand zwischen den Hauptebenen zu vergessen und zu berücksichtigen, dass nur die hintere Hauptebene von Bedeutung ist. Dies entspricht der Einstellung von e = 0, was im Grunde die Näherung der dünnen Linse ist.

Das Festhalten an dieser Annäherung vereinfacht das Lernen der Optik erheblich, da Sie Begriffe wie Hauptebenen, Haupt- oder Knotenpunkte, Objektraum, Bildraum usw. nicht verstehen müssen. Bedenkt, dass:

• Die Annäherung ist für die meisten (nicht makroökonomischen) Zwecke gut genug
• Kenntnisse in Optik sind nur für einen Fotografen auf qualitativer Ebene nützlich, da Sie keine Objektive entwerfen und keine Optikkenntnisse benötigen, um ein großartiger Fotograf zu werden

Es ist verständlich, dass das dünne Objektiv das Modell ist, das Fotografen am häufigsten beigebracht wird. Und doch bricht die Annäherung, wenn es sich um eine komplexe dicke Linse in Makroabständen handelt. Die Antworten, die Ihnen sagen, dass die Brennweite ein Viertel der Entfernung zwischen Motiv und Bild beträgt, veranschaulichen, wie dieses Missverständnis dazu führt, dass Personen falsche Antworten veröffentlichen.

Der Arbeitsabstand wird von der Vorderseite des Objektivs zum Motiv gemessen. Für Ihr EF 100 mm 1: 2,8 L IS USM-Makroobjektiv beträgt der Arbeitsabstand bei minimaler Fokusentfernung (MFD) / voller Vergrößerung ca. 133 mm.

Die Fokusentfernung wird vom Motiv zur Bildebene (Film oder Sensor) gemessen. Für Ihr EF 100 mm 1: 2,8 L IS USM-Makroobjektiv beträgt die Fokusentfernung bei voller Vergrößerung / MFD 300 mm.

Die Brennweiten der meisten Objektive werden gemessen, wenn das Objektiv auf unendlich fokussiert ist (und dann auf die nächste "Standard" -Brennweite gerundet wird). Wenn die Fokusentfernung verringert wird, ändert sich häufig der vom Objektiv bereitgestellte Blickwinkel. Dies wird als Fokusatmung bezeichnet . Das 300-mm-MFD Ihres EF 100-mm-1: 2,8-l-IS-USM-Makros zeigt uns, dass die effektive Brennweite bei 1: 1-Vergrößerung etwa 75 mm beträgt. Dies ist ziemlich häufig bei einem Makroobjektiv mit einer Brennweite im Bereich von 90 bis 105 mm der Fall. Das Tamron 90 mm 1: 2,8 Di VC USD-Makro (F017) verfügt beispielsweise auch über einen MFD von 300 mm bei 1: 1-Vergrößerung.

Zusätzlich wird die Brennweite für eine zusammengesetzte Linse von der Brennweite angenähert, die eine einzelne Linse benötigen würde, um die gleiche Vergrößerung bereitzustellen. Eine zusammengesetzte Linse ist ein System aus mehreren Linsen, die normalerweise in Gruppen angeordnet sind und zusammen als eine einzige Linse wirken. Nahezu jedes im Handel erhältliche Objektiv für Wechselobjektivkamerasysteme sind Verbundobjektive. Ihr EF 100 mm 1: 2,8 L IS-Makro verfügt über 15 Linsenelemente, die in 12 Gruppen angeordnet sind.

Bei den meisten Weitwinkelobjektiven mit Retrofokus-Design befindet sich dieser theoretische einfache Einzellinsenpunkt weit hinter der Vorderseite des Objektivs. Bei Teleobjektiven befindet sich dieser Punkt per Definition vor der Vorderseite des Objektivs.

Bei Fokussierung auf die minimale Fokusentfernung (MFD) von 300 mm befindet sich die Vorderseite Ihres EF 100 mm 1: 2,8 L IS USM-Makros etwa 168 mm vor dem Sensor. Das Sichtfeld und die Vergrößerung, die das Objektiv bei MFD bietet, machen es jedoch effektiv zu einem 75-mm-Objektiv bei dieser Fokusentfernung. Dies bedeutet, dass sich ein einfaches 75-mm-Objektiv für eine 1: 1-Vergrößerung 150 mm vor dem Sensor befinden muss (wodurch es auch 150 mm vom Motiv entfernt ist). Dadurch wird der effektive Mittelpunkt Ihres EF 100 mm 1: 2,8-Makros etwa 18 mm hinter der Vorderseite des Objektivs platziert, wenn Sie auf das MFD fokussiert sind.

Ich glaube, ich vermisse etwas. Kann jemand erklären, wo ich falsch liege?

Wenn Sie Formeln wie die in Ihrer Frage angegebenen anwenden, müssen Sie 75 mm für die Brennweite des Objektivs verwenden, wenn es auf MFD fokussiert ist.