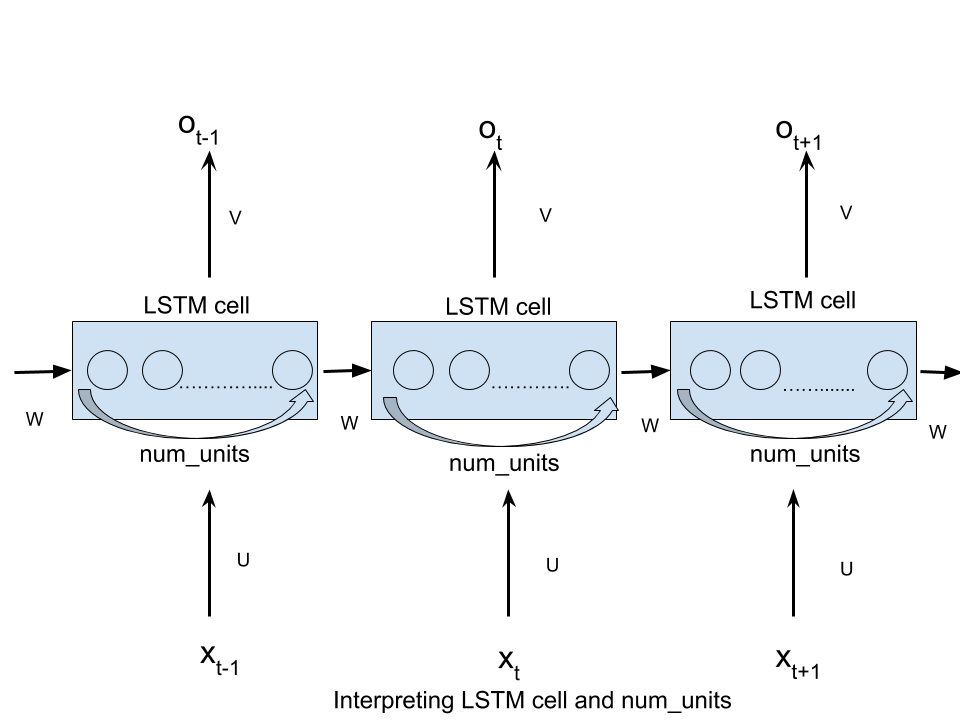
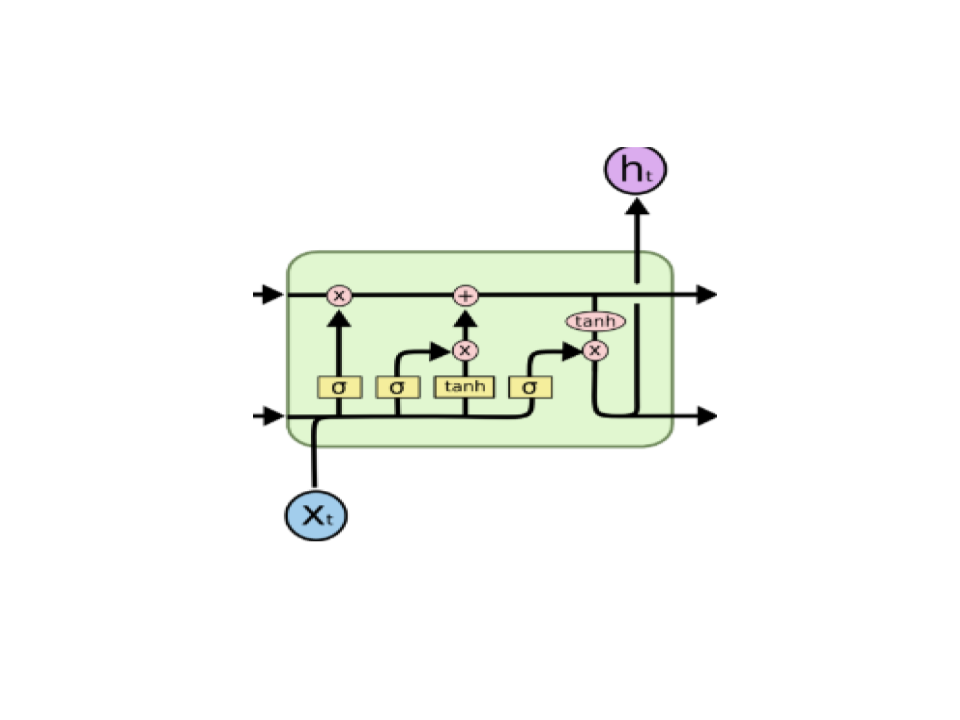
- Ist das richtig?
Ja, die Diagramme sehen für mich beide korrekt aus. Der Schlüssel zum Verständnis beider Diagramme ist, dass die Ein- und Ausgänge einer LSTM-Zelle Vektoren sind.
Die Kreise im ersten Diagramm stellen das Konzept dar, dass die Schicht mehrere einzelne künstliche Neuronen enthält, und das könnte Sie annehmen lassen, dass das zweite Diagramm ein Bild eines dieser Neuronen ist. Wahrscheinlich gibt es mehrere "Neuronen" oder Unterschichten mit unterschiedlichen Rollen innerhalb einer Zelle, da es mehrere Stellen gibt, an denen die Form berechnet wirdf( W.x +b)auftreten und leicht unterschiedliche Rollen spielen. Ich denke, der Begriff "Zelle" bezieht sich auf diese Architektur von Neuronen. Als Abkürzung, wenn ich "Neuron" sage, neige ich dazu, an die Ausgangsstufe der verborgenen Schicht zu denken.
Im zweiten Diagramm arbeiten jedoch alle gezeigten Operationen mit Vektoren. Am wichtigsten ist, dass die Pfeile von links nach rechts im zweiten Diagramm Vektoren des verborgenen Zustands von Zeitschritt zu Zeitschritt von der gesamten Ebene darstellen . Jedes Neuron in der Zelle ist also wiederholt mit jedem anderen Neuron in dieser Zelle verbunden - doppelt so wie in einem LSTM, da LSTMs sowohl einen internen Zellzustand als auch eine Schichtausgabe haben.
- Ist jede Einheit in der Zelle unabhängig von den anderen? Oder teilen sie Informationen?
Um Ihrer Beschreibung der Diagramme zu entsprechen, definieren wir eine "Einheit" als eine Sammlung von jedem Typ von Neuron / Gate, aus dem die Zelle besteht, die theoretisch miteinander verdrahtet werden könnten, um eine funktionierende LSTM-Zellschicht mit einer einzigen zu bilden Skalarzellenzustand und Ausgabewert.
Diese Einheiten sind insofern unabhängig, als jede ihre eigenen Gewichtsparameter hat. Es gibt keine gemeinsamen Parameter für die Verbindungen zwischen dem Eingang und den Einheiten oder für die rekursiven Verbindungen, die den Status von einem Zeitschritt zum nächsten weiterleiten. In diesem Sinne teilen die Einheiten keine Informationen.
Die Verbindungen bedeuten jedoch, dass bei jedem Zeitschritt Eingabedaten und versteckter Zustand plus Ausgabe der letzten Ausgabe aller anderen Einheiten in der Zelle in Berechnungen verwendet werden. Jede Zelleneinheit kann ihren neuen internen Zustand plus ihre Ausgabe auf den Werten aller anderen Ausgaben und internen Zustände von anderen Einheiten in der Zelle basieren. In diesem Sinne teilen die Einheiten Informationen. Ich vermute aus Ihrer Frage, dass es wahrscheinlich dieses zweite Problem ist, über das Sie sich Sorgen machen, da das zweite Diagramm Sie an einen Schaltplan für ein einzelnes Neuron denken lässt, aber wie oben erläutert, ist dies nicht der Fall.
- Stellen Sie sich vor, ich habe die folgende Konfiguration: Anzahl der Abtastwerte = 1000 Anzahl der Zeitschritte = 10 Anzahl der Merkmale = 5 In diesem Fall nimmt jede Einheit in einer Zelle einen Vektor der Größe 5 als Eingabe, oder?
Fast. Jedes Neuron in der Zelle erhält eine Eingabe von 5 vonxplus eine Eingabe der Ausgabe der verborgenen Ebene, h. Wenn in Ihrem Fall die LSTM-Zellgröße 10 wäre, würde jedes Neuron einen kombinierten Vektor von 15 annehmen. Außerdem wird ein zweiter Zellzustandsvektor beibehalten, der in Ihrem Diagramm nicht markiert ist. Dies wird nicht direkt als Eingabe für irgendwelche Neuronen (dh Komponenten der Form) verwendetf( W.x +b)), interagiert aber mit den anderen Werten und kann sich durch die verschiedenen Tore selbst ändern. In Ihrem zweiten Diagramm ist es der oberste Pfeil von links nach rechts.
Aber wie groß wird der Ausgang für eine Einheit sein? 1?
Die Zelle als Ganzes hat die Ausgabe in der Größe, in der Sie die Ebene erstellt haben. Das versucht das Diagramm Nummer 2 zu zeigen. Unter Verwendung unserer Arbeitsdefinition von "Einheit" besteht die Ausgabe jeder Einheit jedoch aus zwei Skalarwerten - der Ausgabe der verborgenen Schicht und dem Zellenzustand -, die Teil ihrer jeweiligen in den Diagrammen gezeigten Vektoren sind.