Jelly ist eine implizite , golforientierte Programmiersprache von unserem eigenen Dennis . Es taucht hier immer häufiger in Antworten auf und schlägt andere Golf-Sprachen wie Pyth und CJam, indem es sowohl eine eigene Codepage als auch ein leistungsfähiges Kettensystem verwendet, um Programme kurz und bündig auszudrücken.

Lassen Sie uns ein paar nützliche Tipps zum Golfen in Jelly sammeln. (Wie immer ein Tipp pro Antwort!)

String-Komprimierung

Wenn Sie nach einem optimierten / automatischen Saitenkompressor suchen, probieren Sie diesen aus .

Probieren Sie es online!

Eine komprimierte Zeichenfolge sieht so aus “...», als ob die Punkte ein Teil der Base-250-codierten Daten sind. Der Dekomprimierungsalgorithmus ist etwas kompliziert: Der Block wird als eine Ganzzahl mit gemischter Basis interpretiert, divmodwobei verschiedene Teile dieser Ganzzahl abgebrochen und daraus eine Zeichenfolge erstellt werden.

Ich habe ein kleines Python 3-Interface erstellt, um Jelly-Strings zu komprimieren:

import dictionary
code_page = '''¡¢£¤¥¦©¬®µ½¿€ÆÇÐÑ×ØŒÞßæçðıȷñ÷øœþ !"#$%&'()*+,-./0123456789:;<=>?@ABCDEFGHIJKLMNOPQRSTUVWXYZ[\]^_`abcdefghijklmnopqrstuvwxyz{|}~¶°¹²³⁴⁵⁶⁷⁸⁹⁺⁻⁼⁽⁾ƁƇƊƑƓƘⱮƝƤƬƲȤɓƈɗƒɠɦƙɱɲƥʠɼʂƭʋȥẠḄḌẸḤỊḲḶṂṆỌṚṢṬỤṾẈỴẒȦḂĊḊĖḞĠḢİĿṀṄȮṖṘṠṪẆẊẎŻạḅḍẹḥịḳḷṃṇọṛṣṭụṿẉỵẓȧḃċḋėḟġḣŀṁṅȯṗṙṡṫẇẋẏż«»‘’“”'''

class Compress(list):
    def character(self, c):
        if c in '\n\x7f¶':
            o = 95
        elif ' ' <= c <= '~':
            o = ord(c)-32
        else:
            raise ValueError(c + " is neither printable ASCII nor a linefeed.")
        self += [lambda z: 3*z+0, lambda z: 96*z+o]; return self
    def string(self, s):
        for c in s: self.character(c)
        return self
    def dictionary(self, w):
        ts = bool(self)
        if w[:1] == ' ': w = w[1:]; ts = not ts
        dct = dictionary.short if len(w) < 6 else dictionary.long
        W, sc = (w, 0) if w in dct else (w[:1].swapcase() + w[1:], 1)
        if W not in dct: raise ValueError(w + " isn't in the dictionary.")
        f = ts or sc; j = (2 if sc else 1) if ts else 0; i = dct.index(W)
        self += [lambda z: 3*z+2, lambda z: 3*z+j] if f else [lambda z: 3*z+1]
        self += [lambda z: 2*z+int(len(w) < 6), lambda z: len(dct)*z+i]
        return self
    def go(self):
        compressed = []; z = 0
        for f in self[::-1]: z = f(z)
        while z:
            c = z % 250
            if c == 0: c = 250
            z = (z - c) // 250
            compressed.append(code_page[c - 1])
        return '“{0}»'.format(''.join(compressed[::-1]))

Verwenden Sie den Kompressor wie folgt.

print(Compress()
      .dictionary('public')
      .dictionary(' static')
      .dictionary(' boolean')
      .string(' is')
      .dictionary('Power')
      .string('Of')
      .dictionary('Ten')
      .string('(')
      .dictionary('long')
      .dictionary(' input')
      .string(') {\n ')
      .dictionary(' return')
      .string('\n   ')
      .dictionary(' input')
      .string(' ==')
      .go())

Compress ist ein String Builder:

• .string(s) Fügt rohe, druckbare ASCII-Zeichen in die Zeichenfolge ein.

  (Jedes Zeichen kostet ungefähr 0,827 komprimierte Bytes.)

• .dictionary(w)Sucht eine Zeichenfolge in Jellys integrierten Wörterbüchern. Sie können die Zeichenfolge mit einem einzelnen Leerzeichen beginnen, wenn Sie eines möchten. Wenn dies vom normalen Verhalten beim Hinzufügen von Zeichenfolgen abweichen oder die Großschreibung eines Wörterbuchworts umkehren muss, werden dementsprechend Flags hinzugefügt.

  (Kostet ungefähr 1.997 Bytes für kurze Wörter, 2.433 Bytes für lange Wörter. Wenn Flags vorhanden sind, addieren Sie 0.199 Bytes.)

Dies ist Teil des Wiki-Tutorials von Jelly .

Ketten

(Dies ist eine Art Nachfolger der Tacit-Programmierung .)

Wie bewertet Jelly eine Kette? Wie bereits erläutert, sind drei Fälle zu berücksichtigen: ob diese Kette niladisch , monadisch oder dyadisch aufgerufen wurde .

1. Niladische Ketten

Dies sind die einfachsten von allen. Um eine Niladenkette zu bewerten, die mit einer Nilade beginnt , wie zum Beispiel α f g h, bewerten Sie die monadische Kette f g han dieser Nilade α. (Vorsichtsmaßnahmen: Wenn die gesamte Kette leer ist, wird stattdessen 0 zurückgegeben. Wenn α es sich nicht um einen Nilad handelt, ersetzen Sie α=0stattdessen use .)

Zum Beispiel 4½wird nur bei ½ausgewertet 4, was ist 2.

2. Monadische Ketten

Monadische Ketten werden von links nach rechts zerlegt, bis keine zu berücksichtigenden Glieder mehr vorhanden sind. Außerdem haben wir hier einige Argumente übergeben ω. Es gibt zwei Fragen zu beantworten:

Was ist der Startwert für diese Bewertung von links nach rechts?

• Wenn unsere Kette mit einer Nilade beginnt αund auf sie null oder mehr Monaden (wie ½), Dyaden-Niladen-Paare (wie +2) und Niladen-Dyaden-Paare (wie 4*) folgen : Wir beginnen mit der Bewertung αund betrachten dann den Rest der Kette .

• Ansonsten gehen wir von dem an diese Kette übergebenen Argument aus ωund betrachten die gesamte Kette.

Wie gehen wir die Kette entlang?

Nennen wir Vden aktuellen Wert - anfangs ist es der oben beschriebene Wert, aber er wird aktualisiert, wenn wir die Kette durchlaufen - und bezeichnen

• Nilads mit Ziffern,
• Monaden mit Kleinbuchstaben,
• Dyaden Operator Symbole +, ×, ÷.

Dann werden die folgenden Muster von oben nach unten verglichen:

                                 ┌───────────┬─────────┐
                                 │ old chain │ new V   │
                                 ╞═══════════╪═════════╡
                                 │ + × 1 ... │ (V+ω)×1 │ *
                                 │ + f ...   │ V+f(ω)  │
                                 │ + 1 ...   │ V+1     │
                                 │ 1 + ...   │ 1+V     │
                                 │ + ...     │ V+ω     │
                                 │ f ...     │ f(V)    │
                                 └───────────┴─────────┘
      (* Only if `...` consists of monads, dyad-nilad pairs, and nilad-dyad pairs.)

Lassen Sie uns das an der Kette ausprobieren +²×.

• +ist kein Nilad, also fangen wir an V = ω.
• Dann hacken wir ab +², passen das zweite Muster an und erhalten V = ω+ω².
• Dann hacken wir ab ×und passen das fünfte Muster an V = (ω+ω²)×ω.
• Die Kette ist jetzt leer, so (ω+ω²)×ωist unser Endergebnis.

3. Dyadische Ketten

Dies sind im Grunde wie monadische Ketten, aber dieses Mal gibt es zwei Argumente, λ(links) und ρ(rechts).

Was ist der Startwert?

• Wenn die Kette mit drei Dyaden beginnt + × %, beginnen wir bei λ+ρund betrachten als × % ...nächstes die Kette .

• Ansonsten gehen wir von λder gesamten Kette aus und betrachten sie.

Wie gehen wir die Kette entlang?

Diesmal sind die Muster

                                 ┌───────────┬─────────┐
                                 │ old chain │ new V   │
                                 ╞═══════════╪═════════╡
                                 │ + × 1 ... │ (V+ρ)×1 │ *
                                 │ + × ...   │ V+(λ×ρ) │
                                 │ + 1 ...   │ V+1     │
                                 │ 1 + ...   │ 1+V     │
                                 │ + ...     │ V+ρ     │
                                 │ f ...     │ f(V)    │
                                 └───────────┴─────────┘
      (* Only if `...` consists of monads, dyad-nilad pairs, and nilad-dyad pairs.)

Lassen Sie uns das an der Kette ausprobieren +×÷½.

• Die Kette beginnt mit drei Dyaden, also fangen wir an V = λ+ρund werfen die weg +.
• Dann hacken wir ab ×÷, passen das zweite Muster an und erhalten V = (λ+ρ)×(λ÷ρ).
• Dann hacken wir ab ½und passen das sechste Muster an V = sqrt((λ+ρ)×(λ÷ρ)).
• Die Kette ist jetzt leer, also sind wir fertig.

Numerische Werte in Sonderfällen

Hier sind einige Sonderfälle für den numerischen Parser von Jelly:

• - bewertet zu -1
• . bewertet zu 0.5
• ȷwertet aus zu 1000( ȷist für wissenschaftliche Notation, zB 2ȷ6ist 2000000)
• ıauswerten zu 1j( ıist für komplexe Zahlen, zB 2ı3ist 2+3j)

Es ist auch erwähnenswert, dass so etwas 4ıeigentlich 4+1jeher ist als 4.

Sie können diese mischen und anpassen, zB:

• -.ist -0.5und -ȷist-1000
• -ıist -1+1j, ı-ist -1jund -ı-ist-1-1j
• .ȷ ist 500.0
• .ıist 0.5+1j, ı.ist 0.5jund .ı.ist0.5+0.5j
• ȷıist 1000+1j, ıȷist 1000jund ȷıȷist1000+1000j

Beachten Sie, dass dies der Fall ȷ-ist 0.1, jedoch keine Bytes mehr gespeichert werden .1. Dann gibt es noch Folgendes, was bereits in der entsprechenden Anzahl von Bytes mit der eingebauten Variablen für 10 ( ⁵) durchgeführt werden kann, aber in dem seltenen Fall nützlich sein kann, dass die eingebaute Variable nicht verfügbar ist oder bei Bedarf gespart werden muss ¤:

• ȷ.ist sqrt(10) ~ 3.162277, .ȷ.ist sqrt(10)/2 ~ 1.5811und ȷ-.ist1/sqrt(10) ~ 0.31162

Optimierter Saitenkompressor

Probieren Sie es online!

In Lynns Beitrag wird genau beschrieben, was komprimierte Zeichenfolgen sind, und es wird ein Kompressor bereitgestellt, der diese komprimierten Zeichenfolgen erzeugt. Während jedoch mit einem Programm in Jelly tüftelt, fand ich es zu kombinieren , zu haben ermüdend .dictionaryund .stringum zusammen mit der korrekten Platzierung der Räume und so weiter und so fort, die kürzestmögliche Zeichenfolge zu erreichen.

Aus diesem Grund habe ich beschlossen, eine Erweiterung für Lynns Skript zu erstellen, die Benutzereingaben aufnimmt und den kürzesten Weg findet, wie sie komprimiert werden können, ohne dass der Benutzer irgendwelche Arbeiten ausführen muss. Das Skript ist ziemlich lang und deshalb habe ich einen TIO-Link hinzugefügt, anstatt den Code selbst.

Das Programm funktioniert durch Komprimieren mit drei verschiedenen Methoden und Bestimmen der kürzesten Methode:

1. Methode 1 codiert einfach jedes Byte der Eingabe zu einem Zeitpunkt, wodurch im Vergleich zu den anderen eher das längste Ergebnis erzielt wird. Selbst wenn die Eingabe sehr kurz ist, können relativ lange Alternativen erstellt werden. Der kürzeste Weg, testder komprimiert werden kann, ist beispielsweise “¡ḌY», während diese Methode “¡⁷ƑKʂ»(2 Byte länger) zurückgibt . Dies funktioniert in der Regel nur, wenn die Zeichenfolge kürzer als 4 Zeichen ist

2. Die zweite Methode zerlegt die Zeichenfolge in Wörter und Interpunktion, da beide auf unterschiedliche Weise zum Kompressor hinzugefügt werden. Wörter, die Teil des Wörterbuchs sind, werden mit der .dictionaryMethode von Lynns Code hinzugefügt , die sie stärker komprimiert, als wenn sie einfach durch Codepunkte hinzugefügt würden. Die Zeichensetzung muss jedoch nach Codepunkten hinzugefügt werden, da sie leider nicht Teil des Wörterbuchs sind.

   Die Interpunktion enthält Leerzeichen. Hier kommt Methode 3 ins Spiel, aber zuerst die Bewertung von Methode 2: Vergleichen wir die Methoden eins und zwei, in denen die Zeichenfolge komprimiert wird Hello, World!(enthält Wörter, Interpunktion und Leerzeichen, ist also perfekt). Komprimieren zeichenweise Ergebnisse in der letzten Folge von “ŒCdẉa÷¹ṂȤƓ(Ẋ)»(15 Bytes lang), die, wie sich herausstellt, länger als die einfachere Möglichkeit zur Ausgabe Hallo, Welt !: “Hello, World!. Schauen wir uns nun Methode zwei an. Dies erzeugt die komprimierte Zeichenfolge, “Ọƥ⁷Ƭė3⁶»die 9 Bytes wiegt, eine große Verbesserung gegenüber der alten. Das kürzeste Hallo, Welt! Programm in Jelly ist 8 Bytes , also kann etwas verbessert werden

3. Hier kommt Methode 3, wodurch sie noch kürzer wird. Wie erwartet ist die Ausgabe für Hello, World natürlich “3ḅaė;œ»das kürzestmögliche Programm. Was macht Methode 3, Methode 2 nicht? Methode 3 kombiniert einzelne Räume zu führenden Räumen, für die der Jelly-Dekomprimierer ein Flag hat. Im Code sowohl für den Kompressor als auch für den Dekomprimierer sehen Sie Code if flag_space: word = ' ' + word, der zeigt, dass führende Leerzeichen a) unterstützt werden und b) bytesparend sind. Daher wird der Stringsplitter aus Methode zwei so angepasst, dass Leerzeichen für sich direkt nach dem String kombiniert werden, um führende Strings zu erstellen. Dies bedeutet, dass Hello, World!analysiert wird als ["Hello", ",", " World", "!"], was, wenn komprimiert, nur 6 Bytes beträgt (8, wenn Begrenzer eingeschlossen). Dies ist fast immer die kürzeste Komprimierungsmethode, mit Ausnahme der "Erweiterung", die ich hinzugefügt habe.

Dies ist der Hauptteil des Programms, aber es gibt noch ein paar weitere Optionen, mit denen die Daten noch stärker komprimiert werden können.

• Das Programm prüft, ob jede komprimierte Version korrekt ist oder nicht, indem es Dennis ' sss- Dekomprimierer verwendet, den Jelly verwendet (gehen Sie direkt zur Quelle).
• Sie können alle verschiedenen komprimierten Zeichenfolgen anzeigen, indem Sie das erste Befehlszeilenargument eingeben --debug, das nicht nur die kürzeste komprimierte Zeichenfolge anzeigt, sondern alle 3 zusammen mit einer Kopie "Dies ist die kürzeste"
• Das Programm behandelt "Nicht-Wörter"

Nicht-Wörter

Nachdem ich diese Nachricht gesehen hatte, fing ich an, an Lynns Kompressor zu arbeiten , machte einen Knack und war frustriert darüber, dass ich nicht den kürzesten Weg fand, ihn zu komprimieren (es sind 29 oder 32 Bytes für den Datensatz). Beim Testen meiner Verbesserungen stellte ich jedoch fest, dass Wörter wie knownsnicht in Jellys Wörterbuch enthalten sind. Aus diesem Grund habe ich mich vorgenommen, einen Weg zu finden, um diese "Nichtwörter" in einem möglichst kurzen Jelly-Code zu komprimieren.

Ich habe eine function ( trim) erstellt, die den String als einen Punkt aufteilt, an dem mindestens einer der Teile des Strings Wörter sind. Zum Beispiel knownswürde aufgeteilt werden ["known", "s"]und das Programm das erste Wort über ein Wörterbuch add ( .dictionary) und den zweiten Teil des Wortes über einen .stringAufruf hinzufügen . Es verbleiben jedoch zwei Randfälle: Zeichenfolgen, in denen keine Wörter enthalten sind (z. B. ajdl), und Nicht-Wörter, in denen Wörter am Ende stehen, z. B. abctest, die von der trimFunktion nicht aufgeteilt werden .

Da es keine Möglichkeit gibt, Wörter in einer Zeichenfolge zu finden, die keine Wörter enthält, besteht die einfachste und kürzeste Möglichkeit, diese zu behandeln, darin, sie Zeichen für Zeichen über einen .stringAufruf hinzuzufügen . So ajdlerhalten würde ergänzt durch .string('ajdl'). Während Nichtwörter, die mit erkannten Wörtern enden, im Wesentlichen den Trimmer aber in umgekehrter Reihenfolge ausführen .dictionaryund .stringauf den Vorwärtstrimmer anwenden und umgekehrt .

Wie sich herausstellt, ist das Trimmen der Zeichenfolge entweder vom Anfang oder vom Ende an natürlich kürzer als das Hinzufügen der einzelnen Zeichen zum Kompressor, wie durch die Eingabe von gezeigt wird abctest this string, was eine Debug-Ausgabe von ergibt

Original        : abctest this string

Optimised       : “¡J+v(p⁸ụƘ$,»
Seperate spaces : “Ç⁴ṭḍµḄ7oeṂdḷp»
No trimmer      : “¤ɦ?Ɓ¢#fḲOạ⁾¶ɼȥƬ»
All characters  : “µẓþ"Y7_ḣṗḢ))9Þ⁴⁺Ẉ²)ɱ»
Non-compressed  : “abctest this string
Shortest        : “¡J+v(p⁸ụƘ$,»
=====

Der Unterschied zwischen der optimalen Ausgabe (die den Trimmer verwendet) und der, die dies nicht tut, ist eine satte (für Jelly) 4 Bytes. Schließlich gibt es Fälle, in denen die Zeichenfolge selbst kürzer ist als jede komprimierte Version, die jetzt berücksichtigt wurde.

Ein großer Verdienst dafür geht natürlich an Lynn, die den Originalkompressor entwickelt hat

Sie können hochgestellte drei bis neun ( ³⁴⁵⁶⁷⁸⁹) verwenden, um einige häufig verwendete Werte abzurufen. Dies hängt jedoch von der Anzahl der Befehlszeilenargumente und bei Verknüpfungen von den Argumenten der Verknüpfungen ab.

• ³ Gibt 100 zurück und funktioniert nur, wenn keine Eingabe vorhanden ist.
• ⁴ Gibt 16 zurück und funktioniert nur, wenn es höchstens einen Eingang gibt.
• ⁵ gibt 10 zurück und funktioniert nur, wenn es höchstens zwei Eingänge gibt.
• ⁶ Gibt ein Leerzeichen zurück, wenn höchstens drei Eingaben vorhanden sind.
• ⁷ Gibt eine neue Zeile zurück, wenn höchstens vier Eingänge vorhanden sind.

Wenn es jedoch fünf Eingänge gibt, hat man Pech.

Kürzlich hat eine neue Version der Sprache den Wert ³auf 100 gesenkt und einige neue Atome eingeführt, die Werte oder (für Links) ihre Argumente zurückgeben.

• ⁸ Gibt überall eine leere Liste zurück, mit Ausnahme von Links, denen ein linkes Argument übergeben wurde.
• ⁹ Gibt überall 256 zurück, außer bei Links, denen ein rechtes Argument übergeben wurde.

Wenn Sie in einem Link sind und Argumente von beiden Seiten an ihn weitergeleitet bekommen, haben Sie jedoch kein Glück.

Missbrauch von String-Bugs

Dank geht an Adnan , der dies zuerst in Schreiben eines Programms zur Elastifizierung von Saiten ausgenutzt hat .

Jelly soll eines Tages eine Zeichenarithmetik erhalten, aber bis dies passiert, können wir die Tatsache ausnutzen, dass Python die meisten arithmetischen Operatoren überlastet und Jelly keine Typprüfung durchführt.

Zum Beispiel

“abcd”Ḥ

soll Ḥmomentan nichts nützliches tun, ist aber da (unhalve) implementiert als

lambda z: z * 2

und arithmetische Atome vektorisieren in der Tiefe 0 (dh sie arbeiten mit Zahlen oder Zeichen), was den obigen Jelly-Code ergibt

['aa', 'bb', 'cc', 'dd']

Achten Sie darauf, dass dabei echte Python-Strings erzeugt werden (ein Typ, den Jelly eigentlich nicht haben sollte), damit er nicht in allen Situationen verwendet werden kann.

Ebenso +/kann es nützlich sein, Zeichenfolgen mit den gleichen Einschränkungen zu verketten.

Optimaler Saitenkompressor

Vor kurzem habe ich fragte Erik die Outgolfer die hinzuzufügen optimierten String Kompressor zu JHT Referenzen Seite , aber sie sagte , dass

sorry, aber das Kompressor scheint nicht vollständig umgesetzt wird
es sagt “ugtestslug”die kürzeste für möglich ist ugtestslug, während “#ṀȮụḄPƇ»auch die Arbeit erledigt

Deshalb entscheide ich mich, den optimalen Saitenkompressor zu implementieren.

Einfacher Ansatz, aber garantiert den kleinstmöglichen Wert (und damit die Anzahl der Bytes) zu finden

Eingaben von stdin, Ausgaben von bis übernehmen stdout. Als Newline kann genau wie beim Originalkompressor ¶oder (wörtliches Newline-Zeichen) eingegeben werden.

Wenn Sie versuchen, es mit viel Interpunktion (z. B. Eingabe ¶-----¶) auszuführen, wird die unkomprimierte Zeichenfolge ausgegeben.

Natürlich ist es Lynn zu verdanken, dass sie den Originalkompressor entwickelt hat .

Dies ist Teil des Wiki-Tutorials von Jelly .

Stillschweigende Programmierung

Jelly ist eine implizite Programmiersprache. Das heißt, Sie definieren Verknüpfungen (Funktionen), indem Sie vorhandene Verknüpfungen zu einer Kette zusammenfassen , ohne explizit auf die betreffenden Argumente einzugehen. Welche Art und Weise die Argumente durch diese Komposition „fließen“, wird durch das Muster definiert, in dem die Links angeordnet sind. Ein Beispiel dafür wird bald gegeben, aber zuerst müssen wir einige Konzepte einführen.

Die arity eines Links ist ein sehr wichtiges Konzept. Alle Atome - die eingebauten wie +und ½- haben feste Aritäten. Links werden je nach Art in drei Kategorien eingeteilt:

• Niladen nehmen keine Argumente an (Arität 0); abgesehen von einigen I / O- und Stateful-Befehlen stellen sie meist konstante Werte dar. Zum Beispiel ist das Literal 3ein Nil.

• Monaden nehmen ein Argument (Arität 1). (Hier besteht keine Verbindung zu funktionalen Programmiermonaden .) Beispielsweise ist ½(Quadratwurzel) eine Monade.

• Dyaden haben zwei Argumente (Arity 2): ein linkes und ein rechtes Argument. Zum Beispiel +ist eine Dyade.

(Mit Adjektiven sagen wir, dass eine Verknüpfung niladisch , monadisch oder dyadisch ist .)

Welche Art von Links definieren wir beim Schreiben eines Programms? Standardmäßig sind sie variabel - das heißt, der Aufrufer muss angeben, wie viele Argumente verwendet werden sollen, und im Fall des Hauptlinks hängt es davon ab, wie viele Argumente das Programm übergeben hat.

Als Beispiel +½dient eine Kette aus +(Addition) und ½(Quadratwurzel). Da die jeweiligen Elemente dieser Kette 2 und 1 sind, bezeichnen wir sie als 2,1-Kette . Der Interpreter hat spezifische Regeln für das Aufteilen von Ketten, basierend auf ihren Aritäten: Diese Regeln schreiben vor, dass ndiese neue Verknüpfung bei einer Eingabe berechnet wird n + sqrt(n). (Sie können +½als "... plus seine Quadratwurzel" lesen . )

Jelly Programming ist also im Wesentlichen die Kunst, diese Regeln gut zu lernen und clevere Ketten zu bilden, die die Arbeit stillschweigend erledigen .

Dies ist Teil des Wiki-Tutorials von Jelly .

Programmstruktur

Jede Zeile in einem Jelly-Programm ist eine Linkdefinition . Links sind grundsätzlich Funktionen. Die unterste Zeile steht für " main": Dies ist der Link, der anhand der in der Befehlszeile übergebenen Argumente ausgewertet wird.

Alle Links außer dem letzten sind Funktionsdefinitionen: Sie können mit Hilfe von Akteuren auf sie verweisen . Zum Beispiel çist „der Link über diese, als binären Operator (Dyade)“ . Betrachten Sie dieses Beispielprogramm , das das Quadrat der Summe seiner Argumente berechnet:

+
ç²

Das ist so ähnlich wie der Pseudocode:

define f:
    the built-in link +
define main:
    apply the dyad f
    square the result

Dies ist Teil des Wiki-Tutorials von Jelly .

Mehrkettenglieder

Erinnern Sie sich, als ich schrieb, dass Sie einen Link definieren, indem Sie eine Kette von anderen Links bilden? Ich habe nicht die ganze Wahrheit gesagt: In Wirklichkeit handelt es sich um einen zweischichtigen Prozess. Ein Glied ist eine Kette von Ketten , und die äußere Kette hat standardmäßig nur eine Einheitslänge.

Betrachten Sie dieses Programm:

C+H

Das ist Ergänzung plus die Hälfte . Es nimmt einen Eingabewert nund berechnet (1-n)+(n/2). Nicht zu aufregend, ich weiß. Aber die Struktur ist wirklich so:

Das von uns geschriebene Glied ist selbst eine Kette, die eine einzelne Kette enthält.

Angenommen, wir möchten (1-n)+(1-n)(n/2)stattdessen berechnen . Die dyadische Kette +×würde funktionieren: Nach den Regeln für die Verkettung berechnet sie λ+(λ×ρ), was genau so aussieht, wie wir es brauchen. Doch einfach ersetzt +durch +×in unserem Programm nicht tun: C+×Hein 1,2,2,1-Kette - Komplement, dann fügen Sie (das Argument), dann multiplizieren um die Hälfte - Berechnung ((1-n)+n)×(n/2).

Wir wollen Jelly zu behandeln +×als eine Einheit, und machen eine 1,2,1-Kette der Unterketten C, +×und H. Mehrkettenglieder machen wir genau das! Um sie zu konstruieren, verwenden wir die Kettenseparatoren øµð : In der obigen Abbildung würden sie ein neues blaues Rechteck der Arität 0, 1 bzw. 2 einführen. In unserem Fall können wir die Ketten wie gewünscht gruppieren, indem wir Folgendes schreiben Cð+×µH:

Es gibt keine Möglichkeit, diese Dinge noch weiter zu verschachteln. Sie müssen stattdessen mehrere Links definieren.

Wenn TMTOWTDI, wählen Sie diejenige aus, die zu Ihrer Kette passt.

Einer der Vorteile einer stillschweigenden Sprache ist, dass Sie normalerweise ohne variable Referenzen davonkommen können. Dies funktioniert jedoch nur, wenn die Glieder in Ihrer Kette die richtigen Eigenschaften haben.

Beispielsweise ist die einfache Methode, die Summe aller Arrays in einem 2D-Array zu berechnen

S€

Dies ordnet das Summenatom allen Elementen des Arrays zu.

Angenommen, Sie haben eine monadische Kette, die aus dem Atom besteht

*

die jedes x eines 2D-Arrays auf x ^x abbildet . Zum Beispiel würde für A = [[1, 2], [3, 1], [2, 3]] das Aufrufen der Kette [[1, 4], [27, 1], [4, 27] ergeben. .

Nun wollen wir die Summe jedes Paares nehmen. Unglücklicherweise,

*S€

funktioniert nicht mehr, da *es sich nicht mehr wie ein Haken verhält ( A selbst als richtiges Argument verwenden), sondern wie eine Abzweigung , was bedeutet, dass es zuerst S€auf A angewendet wird und das Ergebnis das richtige Argument von ist *.

Dies zu beheben ist einfach genug:

*¹S€
*⁸S€

Beide erzeugen das gewünschte Ergebnis: *¹Ist eine Gabelung, in der ¹die Identitätsfunktion steht, und *⁸ist eine Spitze , in ⁸der auf das linke Argument der Kette verwiesen wird ( A ).

Es gibt jedoch eine Möglichkeit, ein Byte zu speichern! Die Spitze ḅ1(convert von unären zu integer) berechnet auch die Summe jeden Array in A ^A , aber im Gegensatz zu S€, ḅist ein dyadischer Link.

Die Kette

*ḅ1

gibt [5, 28, 31] zurück (wie gewünscht); da ḅist dyadisch, *haken statt gabeln

Ganzzahlige Komprimierung

Die Komprimierung von Zeichenfolgen ist nützlich, wenn Sie Text in Englisch erstellen. Wenn Sie jedoch andere Arten von Daten komprimieren müssen, ist dies ziemlich ineffektiv. Aus diesem Grund ist es am besten, eine große feste Konstante in Ihrem Programm als Ganzzahl zu speichern.

Da Jelly nun eine eigene Codepage als Konstante hat, wird der Komprimierungsalgorithmus für Ganzzahlen am einfachsten in Jelly selbst ausgedrückt:

ḃ250ịØJ”“;;”’ṄV

Probieren Sie es online!

(Das obige Programm enthält auch eine Überprüfung, um den Wert anzuzeigen, auf den die Ganzzahl dekomprimiert wird.)

Sie können nicht nur eine Ganzzahl als Ganzzahl verwenden, sondern auch eine Zeichenfolge erstellen, indem Sie eine Basiskonvertierung durchführen und dann in ein Buchstabenalphabet indexieren. Das ṃAtom automatisiert diesen Prozess und ist recht nützlich, da es den gesamten Dekomprimierungsprozess (mit Ausnahme des Alphabets, in das dekomprimiert wird) in einem einzelnen Byte beschreiben kann.

Verwenden Sie äußere Produkte, um nützliche Ganzzahlmatrizen zu erstellen

Hier ist eine Zusammenfassung dieses Beitrags mit etwas besserer HTML-Tabellenformatierung.

Das äußere Produkt quick þkann an Dyaden angehängt werden und bewirkt, dass die Dyade in ihren linken und rechten Argumenten auf jedes Elementpaar einwirkt. Es ist eine Abkürzung für €Ð€. Wenn wir zum Beispiel den Code hätten [1,2]+€Ð€[0,10], könnten wir ihn verkürzen [1,2]+þ[0,10] und sie würden beide ergeben [[1,2],[11,12]]. Ich werde eine Dyade mit þangewendet (wie +þ) als äußere Produktdyade bezeichnen.

Wenn eine Ganzzahl eines der Argumente einer Dyade des äußeren Produkts ist, nimmt Jelly zuerst den Bereich dieser Zahl und verwendet dann das Ergebnis als Argument. In diesem Wissen kann das obige Beispiel weiter verkürzt werden 2+þ[0,10]. Dies gilt sowohl für die linken als auch für die rechten Argumente einer äußeren Produktdyade.

Einige Dyaden des äußeren Produkts ergeben, wenn sie monadisch auf eine Ganzzahl einwirken, bestimmte Ganzzahlmatrizen, die beim Golfen nützlich sein können (insbesondere ASCII-Kunst-Herausforderungen), aber viele Bytes benötigen, um sich anders zu konstruieren. Beispielsweise ergibt sich =þbei Anwendung auf eine ganze Zahl neine n×nIdentitätsmatrix. Online versuchen =þ!

Nachfolgend finden Sie eine Tabelle der Dyaden und die Art der Matrizen, die sie ergeben, wenn sie zu Dyaden des äußeren Produkts verarbeitet und monadisch auf eine ganze Zahl einwirken. Dyaden, die in derselben Reihe aufgeführt sind, ergeben dieselben Matrizen. Es gibt Dyaden Ich habe nicht in der Tabelle enthalten wie &, |, %, w, ẇund ḍdass auch Integer - Matrizen erzeugen aber ihre Muster sind nicht so einfach und würde wahrscheinlich in weniger Situationen nützlich sein. Online versuchen wþ!

+ ------------------------------------------------- ---- +
| Dyad | Resultierende Matrix | Beispiel |
+ ------------------------------------------------- ---- +
| = ⁼ | | 1 0 0 |
| ċ | Identitätsmatrix | 0 1 0 |
| | | 0 0 1 |
+ ------------------------------------------------- ---- +
| | Elemente über der Diagonale sind 1, | 0 1 1 |
| <| Alle anderen Elemente sind 0 | 0 0 1 |
| | | 0 0 0 |
+ ------------------------------------------------- ---- +
| | Elemente unterhalb der Diagonale sind 1, | 0 0 0 |
| > | Alle anderen Elemente sind 0 | 1 0 0 |
| | | 1 1 0 |
+ ------------------------------------------------- ---- +
| | Diagonale Elemente sind 0, | 0 1 1 |
| n ⁻ | Nicht diagonale Elemente sind 1 | 1 0 1 |
| | | 1 1 0 |
+ ------------------------------------------------- ---- +
| a ȧ | | 1 1 1 |
| ṛ ị | Zeilenindex jedes Elements | 2 2 2 |
| | | 3 3 3 |
+ ------------------------------------------------- ---- +
| o ḷ | | 1 2 3 |
| ȯ | Spaltenindex jedes Elements | 1 2 3 |
| | | 1 2 3 |
+ ------------------------------------------------- ---- +
| | Hauptdiagonale ist 0, obere | 0 1 2 |
| _ | Diagonalen sind 1, 2 ..., niedriger | -1 0 1 |
| | Diagonalen sind -1, -2 ... | -2 -1 0 |
+ ------------------------------------------------- ---- +
| | Hauptdiagonale ist 0, niedriger | 0 -1 -2 |
| _ @ | Diagonalen sind 1, 2 ..., obere | 1 0 -1 |
| | Diagonalen sind -1, -2 ... | 2 1 0 |
+ ------------------------------------------------- ---- +
| | Hauptdiagonale ist 0, obere | 0 1 2 |
| ạ | und untere Diagonalen sind 1, | 1 0 1 |
| | 2, 3 ... | 2 1 0 |
+ ------------------------------------------------- ---- +
| | | 2 3 4 |
| + | Zeilenindex plus Spaltenindex | 3 4 5 |
| | | 4 5 6 |
+ ------------------------------------------------- ---- +
| | Minimum der Reihe | 1 1 1 |
| «| und Spaltenindizes | 1 2 2 |
| | | 1 2 3 |
+ ------------------------------------------------- ---- +
| | Maximum der Reihe | 1 2 3 |
| »| und Spaltenindizes | 2 2 3 |
| | | 3 3 3 |
+ ------------------------------------------------- ---- +

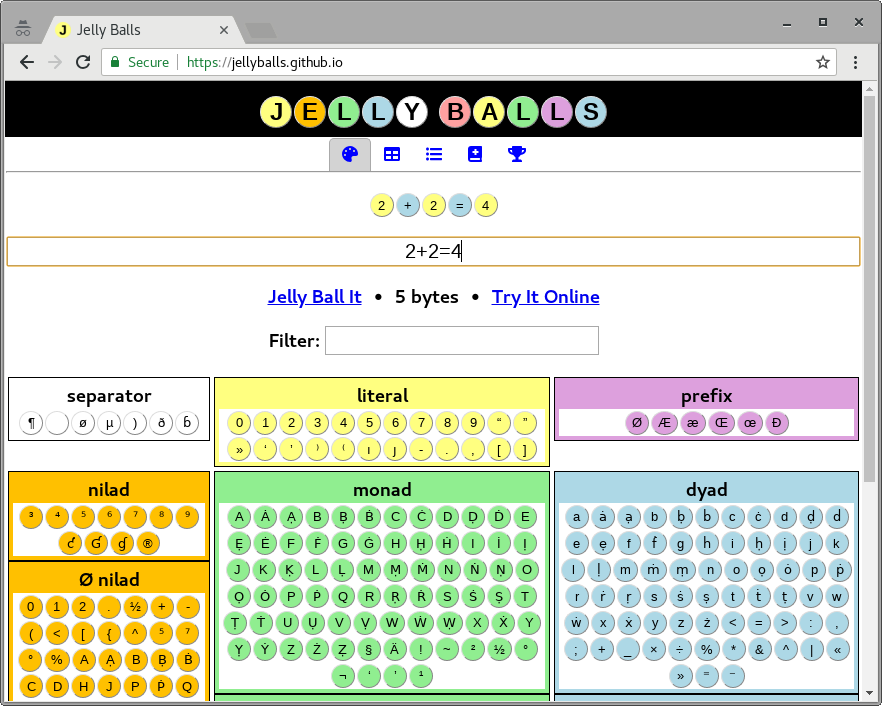
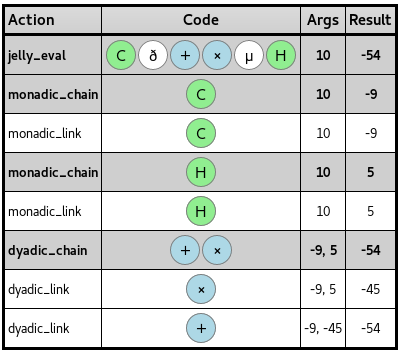
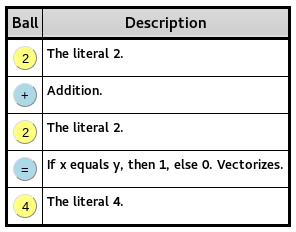
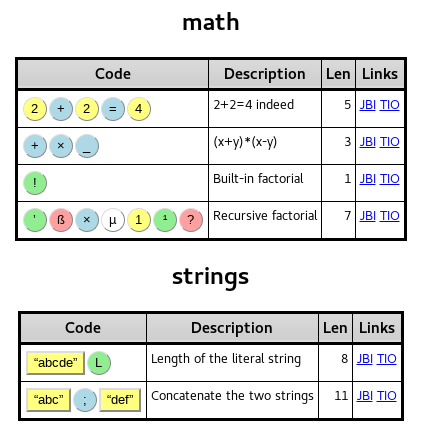
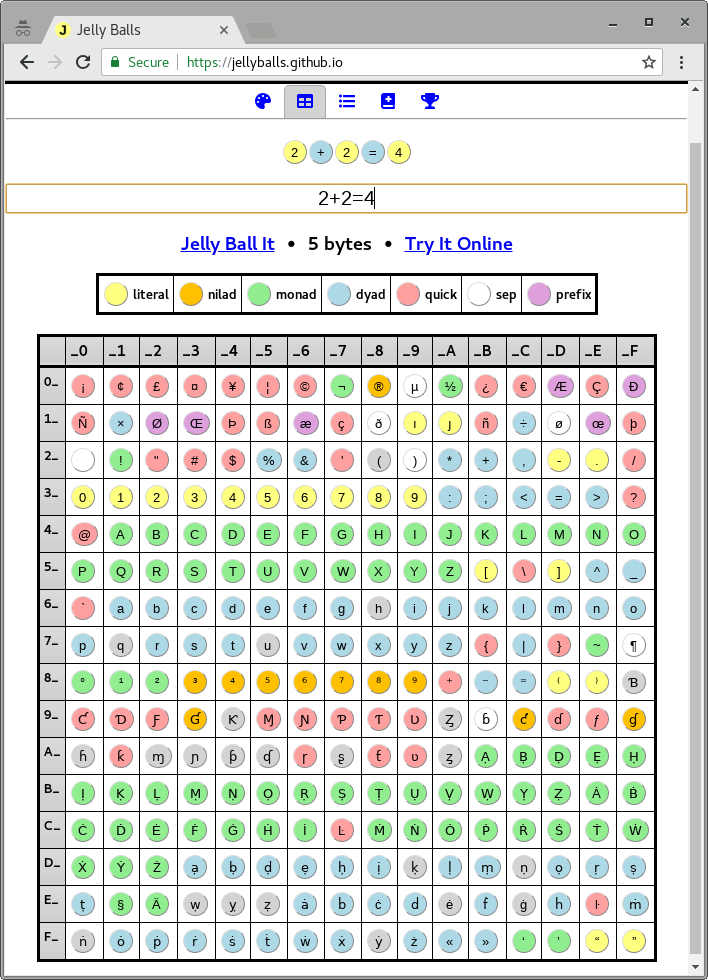
Listet Befehle und Literale auf

Wenn Sie versuchen, viele der nicht vektorisierenden Listenbefehle in einem Literal n oder einer Liste von Literalen zu verwenden z , wird der Listenbefehl zuerst in eine Liste konvertiert und führt dann den Befehl in dieser Liste aus.

Diese Befehle werden durch Aufrufe der iterableFunktion in jelly.py angezeigt .

def iterable(argument, make_copy = False, make_digits = False, make_range = False):
    the_type = type(argument)
    if the_type == list:
        return copy.deepcopy(argument) if make_copy else argument
    if the_type != str and make_digits:
        return to_base(argument, 10)
    if the_type != str and make_range:
        return list(range(1, int(argument) + 1))
    return [argument]

Hier sind einige unvollständige Listen der Funktionen dieser Listenbefehle.

Wraps in einer Liste

Die einfachste Rückkehr von iterable, um das Argument in eine Liste zu setzen und die von der Funktion zu verarbeitende zurückzugeben. Dies ist der Fall, wenn das Argument noch keine Liste ist, eine Zeichenfolge ist und iterabledie Argumente keine anderen Methoden erfordern.

-------------------------------------------------------------------------------
| Command | Description     | Process                       | Effect          |
-------------------------------------------------------------------------------
| F       | Flattens a list | 4953F -> [4953]F -> [4953]    | Same as W       |
-------------------------------------------------------------------------------
| G       | Format a list   | 4953G -> [4953]G -> [4953]    | Same as W       |
|         | as a grid       |                               |                 |
-------------------------------------------------------------------------------
| I       | Increments      | 4953I -> [4953]I -> <nothing> | Empty list      |
-------------------------------------------------------------------------------
| S       | Sums a list     | 4953S -> [4953]S -> 4953      | Same as ¹       |
-------------------------------------------------------------------------------
| Ṭ       | Boolean array,  | 4Ṭ -> [4]Ṭ -> [0, 0, 0, 1]    | n-1 zeroes,     |
|         | 1s at indices   |                               | 1 at end        |
-------------------------------------------------------------------------------
| Ụ       | Sort indices by | 4Ụ -> [4]Ụ -> [1]             | Yields [1]      |
|         | by their values |                               |                 |
-------------------------------------------------------------------------------
| Ė       | Enumerate list  | 4Ė -> [4]Ė -> [[1, 4]]        | Yields [[1, n]] |
-------------------------------------------------------------------------------
| Ġ       | Group indices   | 4Ġ -> [4]Ġ -> [[1]]           | Yields [[1]]    |
|         | by values       |                               |                 |
-------------------------------------------------------------------------------
| Œr      | Run-length      | 4Œr -> [4]Œr -> [[4, 1]]      | Yields [[n, 1]] |
|         | encode a list   |                               |                 |
-------------------------------------------------------------------------------

In Basis 10 konvertieren

Die Funktionen hier rufen iterableauf, um eine Zahl in eine Liste ihrer Ziffern umzuwandeln Dund dann mit diesen Ziffern auszuführen.

-------------------------------------------------------------------------
| Command | Description     | Process                      | Effect     |
-------------------------------------------------------------------------
| Q       | Unique elements | 299Q -> [2, 9, 9]Q -> [2, 9] | Unique     |
|         | ordered by      |                              | digits     |
|         | appearance      |                              | of n       |
-------------------------------------------------------------------------
| Ṛ       | Non-vectorized  | 4953Ṣ -> [4, 9, 5, 3]Ṛ       | Reverses D |
|         | reverse         | -> [3, 5, 4, 9]              |            |
-------------------------------------------------------------------------
| Ṣ       | Sort a list     | 4953Ṣ -> [4, 9, 5, 3]Ṣ       | Sorts D    |
|         |                 | -> [3, 4, 5, 9]              |            |
-------------------------------------------------------------------------

In Liste mit Bereich konvertieren

Die Funktionen hier konvertieren eine Zahl in den Bereich R = [1 ... n]und werden dann in diesem Bereich ausgeführt.

-----------------------------------------------------------------------------------------
| Command | Description       | Process                             | Effect            |
-----------------------------------------------------------------------------------------
| X       | Random element    | 4R -> [1 ... 4]X -> 2               | Random element    |
|         |                   |                                     |  of R             |
|         |                   |                                     |                   |
-----------------------------------------------------------------------------------------
| Ḋ       | Dequeue from list | 4R -> [1 ... 4]Ḋ -> [2, 3, 4]       | Range [2 ... n]   |
-----------------------------------------------------------------------------------------
| Ṗ       | Pop from list     | 4Ṗ -> [1 ... 4]Ṗ -> [1, 2, 3]       | Range [1 ... n-1] |
-----------------------------------------------------------------------------------------
| Ẇ       | Sublists of list  | 4Ẇ -> [1 ... 4]Ẇ                    | All sublists of R |
|         |                   | -> [[1], [2], [3], [4], [1, 2],     |                   |
|         |                   |     [2, 3], [3, 4], [1, 2, 3],      |                   |
|         |                   |     [2, 3, 4], [1, 2, 3, 4]]        |                   |
-----------------------------------------------------------------------------------------
| Ẋ       | Shuffle list      | 4Ẋ -> [1 ... 4]Ẋ -> [2, 1, 3, 4]    | Shuffles R        |
-----------------------------------------------------------------------------------------
| Œ!      | All permutations  | 3Œ! -> [1, 2, 3]Œ!                  | All permutations  |
|         | of a list         | -> [[1, 2, 3], [1, 3, 2],           | of R              |
|         |                   |     [2, 1, 3], [2, 3, 1],           |                   |
|         |                   |     [3, 1, 2], [3, 2, 1]]           |                   |
-----------------------------------------------------------------------------------------
| ŒḄ      | Non-vectorized    | 4ŒḄ -> [1 ... 4]ŒḄ                  | Bounces R         |
|         | bounce,           | -> [1, 2, 3, 4, 3, 2, 1]            |                   |
|         | z[:-1] + z[::-1]  |                                     |                   |
-----------------------------------------------------------------------------------------
| Œc      | Unordered pairs   | 4Œc -> [1 ... 4]Œc                  | Unordered pairs   |
|         | of a list         | -> [[1, 2], [1, 3], [1, 4], [2, 3], | of R              |
|         |                   |     [2, 4], [3, 4]]                 |                   |
-----------------------------------------------------------------------------------------
| Œċ      | Unordered pairs   | 4Œċ -> [1 ... 4]Œċ                  | Unordered pairs   |
|         | with replacement  | -> [[1, 1], [1, 2], [1, 3], [1, 4], | with replacement  |
|         | of a list         |     [2, 2], [2, 3], [2, 4], [3, 3], | of R              |
|         |                   |     [3, 4], [4, 4]]                 |                   |
-----------------------------------------------------------------------------------------
| ŒP      | Powerset of       | 3ŒP -> [1 ... 3]                    | Powerset of R     |
|         | a list            | -> ['', [1], [2], [3], [1, 2],      |                   |
|         |                   |     [1, 3], [2, 3], [1, 2, 3]]      |                   |
-----------------------------------------------------------------------------------------
| Œp      | Cartesian         | 4,2Œp -> [[1 ... 4], [1 ... 2]]Œp   | Cartesian product |
|         | product of z's    | -> [[1, 1], [1, 2], [2, 1], [2, 2], | of [1 ... z[i]]   |
|         | items             |     [3, 1], [3, 2], [4, 1], [4, 2]] | for i in z        |
-----------------------------------------------------------------------------------------

Es lohnt sich manchmal, von der Standardeingabe zu lesen, wenn genau zwei Eingaben vorhanden sind

Jelly ist für die Eingabe von Befehlszeilenargumenten optimiert. Es ist jedoch auch für das Schreiben von Monaden anstelle von Dyaden optimiert. Bei Dyaden gibt es so viele mögliche Bedeutungen für jedes eingebaute Element, dass Sie häufig Zeichen für die Disambiguierung ausgeben müssen, während bei Monaden in der Regel viele Möglichkeiten bestehen, dasselbe auszudrücken.

Als solcher, wenn man nur einmal einen von zwei Eingängen zu verwenden, und das Problem ist, dass es nicht so leicht kann implizit aus gelesen werden ⁴(dh Sie müssen entweder die machen ⁴explizite oder sonst ein Zeichen ausgeben }, @oder dergleichen) Ziehen Sie in Betracht, es von der Standardeingabe zu lesen, Ɠanstatt es in der Befehlszeile zu platzieren. Auf diese Weise können Sie die Eingabe genau dort platzieren, wo Sie sie benötigen Ɠ, und gleichzeitig sicherstellen, dass alle anderen impliziten Eingaben von Ihren anderen Eingaben übernommen werden. Das kostet ein Byte und spart ein Byte. Je nach Problem kann es durchaus sein, dass Sie ein zweites Byte einsparen, indem Sie mehr Spielraum für die Neuordnung des Codes haben.

Es gibt mehrere nicht naheliegende Möglichkeiten, die Eigenschaften eines Arguments mithilfe von zu überprüfen Ƒ. Nachfolgend einige. Ich verließ aus vielen Nutzungen dieses schnell (zB AƑ, ŒuƑ, 3Ƒ) weil sie bereits die einfachstenen Methoden ihr Verhalten zu erreichen.

OƑ  Is number?
ỌƑ  Is character? (errors on negative numeric input)
ḂƑ  Between 0 and 2? 0<=x<2 (python). <2aAƑƊ or of course ⁼Ḃ$ in Jelly.
ḞƑ  Is integer?
UƑ  Like `ŒḂ`, but checks if all sublists of depth 1 are palindromes.
ṠƑ  Is one of -1, 0, 1? (e-r1¤$)

Fühlen Sie sich frei, dies zu bearbeiten, um weitere interessante Fälle hinzuzufügen.

Sie können einen Online - Editor versuchen wollen Jelly Ball entwickelt , um einfach zu bauen Code in Jelly Sprache .

Die Funktionen umfassen:

• Befehlspalette mit allen Atomen und Syntaxzeichen, sortiert nach Typ
• Online-Parser, der Literale und 2-Byte-Atome im Code erkennt
• Vereinfachter Jelly-Interpreter im Browser zum Ausführen Ihres Jelly-Codes auf der Webseite in Javascript
• Direkte Links zum Übertragen des Codes in TIO oder eine andere Jelly Balls-Sitzung
• Automatische Hinweise
• Optimiert für mobile Geräte

Probieren Sie es aus: https://jellyballs.github.io

• Detaillierter Trace-Bericht mit Argumenten und Ergebnissen aller ausgeführten Schritte

• Code-Bericht mit Beschreibung aller Schritte

• Rezeptseite mit Jelly-Beispielen

• Interaktive Codepage mit 256 Jelly-Zeichen