Ich bin einer der Autoren von Gimli. Wir haben bereits eine 2-Tweet-Version (280 Zeichen) in C, aber ich würde gerne sehen, wie klein sie werden kann.
Gimli ( Papier , Webseite ) ist ein Entwurf für kryptografische Permutation mit hoher Geschwindigkeit und hohem Sicherheitsniveau, der auf der Konferenz über kryptografische Hardware und eingebettete Systeme (CHES) 2017 (25.-28. September) vorgestellt wird.
Die Aufgabe
Wie immer: Die kleinteilige, nutzbare Implementierung von Gimli in der Sprache Ihrer Wahl.
Es sollte in der Lage sein, 384 Bits (oder 48 Bytes oder 12 vorzeichenlose Int ...) als Eingabe zu verwenden und das Ergebnis von Gimli, das auf diese 384 Bits angewendet wurde, zurückzugeben (kann an Ort und Stelle geändert werden, wenn Sie Zeiger verwenden) .
Die Eingabeumwandlung von Dezimal, Hexadezimal, Oktal oder Binär ist zulässig.
Mögliche Eckfälle
Die Ganzzahlkodierung wird als Little-Endian-Kodierung angenommen (z. B. was Sie wahrscheinlich bereits haben).
Sie können umbenennen Gimliin , Gaber es muss noch ein Funktionsaufruf sein.
Wer gewinnt?
Das ist Code-Golf, also gewinnt die kürzeste Antwort in Bytes! Es gelten selbstverständlich Standardregeln.
Eine Referenzimplementierung ist unten angegeben.
Hinweis
Einige Bedenken wurden laut:
"hey gang, bitte implementiere mein programm kostenlos in anderen sprachen, damit ich nicht muss" (danke an @jstnthms)
Meine Antwort lautet wie folgt:
Ich kann es leicht in Java, C #, JS, Ocaml tun ... Es ist mehr für den Spaß. Derzeit haben wir (das Gimli-Team) es auf AVR, Cortex-M0, Cortex-M3 / M4, Neon, SSE, SSE-entrollt, AVX, AVX2, VHDL und Python3 implementiert (und optimiert). :)
Über Gimli
Der Staat
Gimli wendet eine Folge von Runden auf einen 384-Bit-Zustand an. Der Zustand wird als Parallelepiped mit den Dimensionen 3 × 4 × 32 oder äquivalent als 3 × 4-Matrix von 32-Bit-Wörtern dargestellt.
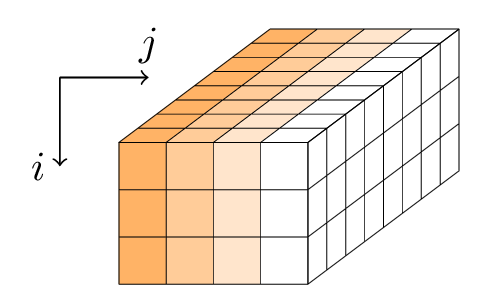
Jede Runde ist eine Folge von drei Operationen:
- eine nichtlineare Schicht, insbesondere eine 96-Bit-SP-Box, die auf jede Spalte angewendet wird;
- in jeder zweiten Runde eine lineare Mischschicht;
- in jeder vierten Runde eine ständige Ergänzung.
Die nichtlineare Schicht.
Die SP-Box besteht aus drei Unteroperationen: Rotation des ersten und des zweiten Wortes; eine nichtlineare T-Funktion mit 3 Eingängen; und ein Tausch des ersten und dritten Wortes.
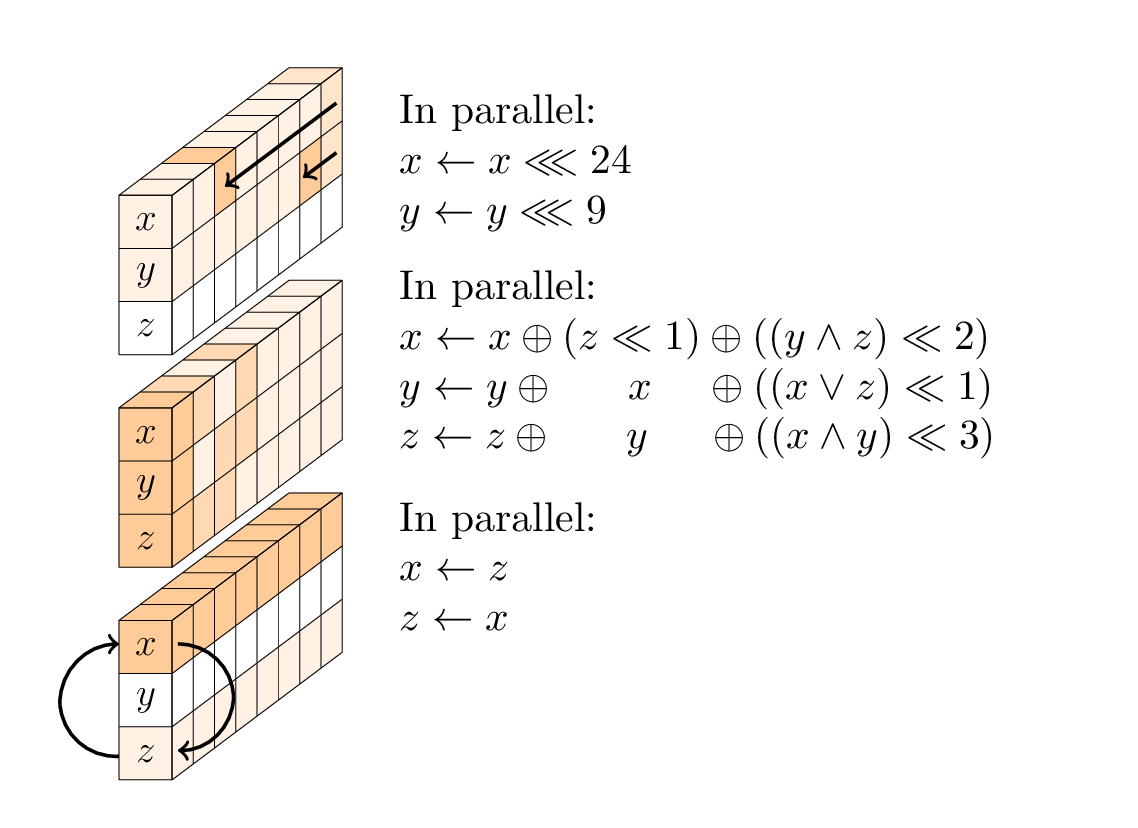
Die lineare Schicht.
Die lineare Ebene besteht aus zwei Swap-Operationen, nämlich Small-Swap und Big-Swap. Small-Swap tritt alle 4 Runden ab der ersten Runde auf. Big-Swap erfolgt alle 4 Runden ab der 3. Runde.

Die runden Konstanten.
Es gibt 24 Runden in Gimli, nummeriert 24,23, ..., 1. Wenn die Rundenzahl r 24,20,16,12,8,4 ist, XOREN wir die Rundenkonstante (0x9e377900 XOR r) zum ersten Zustandswort.
Bezugsquelle in C
#include <stdint.h>
uint32_t rotate(uint32_t x, int bits)
{
if (bits == 0) return x;
return (x << bits) | (x >> (32 - bits));
}
extern void gimli(uint32_t *state)
{
int round;
int column;
uint32_t x;
uint32_t y;
uint32_t z;
for (round = 24; round > 0; --round)
{
for (column = 0; column < 4; ++column)
{
x = rotate(state[ column], 24);
y = rotate(state[4 + column], 9);
z = state[8 + column];
state[8 + column] = x ^ (z << 1) ^ ((y&z) << 2);
state[4 + column] = y ^ x ^ ((x|z) << 1);
state[column] = z ^ y ^ ((x&y) << 3);
}
if ((round & 3) == 0) { // small swap: pattern s...s...s... etc.
x = state[0];
state[0] = state[1];
state[1] = x;
x = state[2];
state[2] = state[3];
state[3] = x;
}
if ((round & 3) == 2) { // big swap: pattern ..S...S...S. etc.
x = state[0];
state[0] = state[2];
state[2] = x;
x = state[1];
state[1] = state[3];
state[3] = x;
}
if ((round & 3) == 0) { // add constant: pattern c...c...c... etc.
state[0] ^= (0x9e377900 | round);
}
}
}Tweetbare Version in C
Dies ist möglicherweise nicht die kleinste verwendbare Implementierung, aber wir wollten eine C-Standardversion (also keine UB und "verwendbar" in einer Bibliothek).
#include<stdint.h>
#define P(V,W)x=V,V=W,W=x
void gimli(uint32_t*S){for(long r=24,c,x,y,z;r;--r%2?P(*S,S[1+y/2]),P(S[3],S[2-y/2]):0,*S^=y?0:0x9e377901+r)for(c=4;c--;y=r%4)x=S[c]<<24|S[c]>>8,y=S[c+4]<<9|S[c+4]>>23,z=S[c+8],S[c]=z^y^8*(x&y),S[c+4]=y^x^2*(x|z),S[c+8]=x^2*z^4*(y&z);}Vektor testen
Die folgende Eingabe wurde generiert von
for (i = 0;i < 12;++i) x[i] = i * i * i + i * 0x9e3779b9;und "gedruckte" Werte von
for (i = 0;i < 12;++i) {
printf("%08x ",x[i])
if (i % 4 == 3) printf("\n");
}somit:
00000000 9e3779ba 3c6ef37a daa66d46
78dde724 1715611a b54cdb2e 53845566
f1bbcfc8 8ff34a5a 2e2ac522 cc624026
sollte zurückkehren:
ba11c85a 91bad119 380ce880 d24c2c68
3eceffea 277a921c 4f73a0bd da5a9cd8
84b673f0 34e52ff7 9e2bef49 f41bb8d6
-roundstatt --roundbedeutet , dass es nie endet. Die Konvertierung --in einen Bindestrich wird im Code wahrscheinlich nicht empfohlen :)