Endgültiges Ergebnis der Beschleunigung und Verzögerung der Gezeiten

Ich weiß also, dass der Mond eine Gezeitenbeschleunigung von der Erde erfährt. Und nach dem, was ich gelesen habe, wäre der Mond in etwa 50 Milliarden Jahren geosynchron, wenn nicht die Sonne die Ozeane wegkochen und beide zuerst verschlingen würde.

Ich war neugierig, ob eine Gezeitenbeschleunigung jemals dazu führen könnte, dass ein Satellit entkommt, und eine kurze Antwort scheint zu sein: Ja, das ist möglich. Ist das richtig? Und wenn ja, welche Faktoren tragen dazu bei?

1. Ein schneller rotierender Planet führt auch dazu, dass die Gezeiten weiter vorne liegen und mehr Energie zu verlieren ist, bevor er vollständig gesperrt wird. Sehr eng verwandt umkreist ein weiter entfernter Satellit langsamer, was zu weiter entfernten Gezeiten führt und weniger Energie benötigt, um zu entkommen. Dieser scheint offensichtlich: Je schneller sich der Planet noch dreht, während der Satellit weiter entfernt ist, desto wahrscheinlicher ist es, dass er entkommt.
2. Ein flüssigerer Planet würde stärkere Gezeiten erfahren, was ihn wieder schneller verlangsamen würde, aber den Satelliten definitiv schneller beschleunigen würde. Eine viskosere Flüssigkeit als Wasser würde schwächere Gezeiten erfahren, aber ich denke, sie wären weiter vorne. Ich denke, mehr Flüssigkeit ist definitiv effektiver, aber es scheint weniger offensichtlich als der erste Punkt.
3. Ein größerer Planet würde seine Umlaufbahn durch Gezeitenbeschleunigung weniger verlangsamen, aber einen stärkeren Zug haben, um zu entkommen. Ein größerer Satellit würde stärkere Gezeiten und mehr Gezeitenkraft verursachen, würde jedoch mehr Kraft zum Beschleunigen erfordern und den Planeten schneller verlangsamen. Ich kann wirklich nicht sagen, welche die stärkere Wirkung hat ...

Das ist also Frage 1: Ist es wirklich möglich, dass die Gezeitenbeschleunigung einen Satelliten in den Weltraum wirft, bevor der Planet gezeitengesperrt ist, und wenn ja, wirkt sich entweder die Größe der Objekte darauf aus oder nur auf die Fließfähigkeit und die relativen Perioden?

Dann wunderte ich mich über die Verzögerung der Gezeiten und den Absturz auf den Planeten. Es scheint offensichtlich, dass jeder Satellit, der rückläufig umkreist, niemals aufhören würde, sich zu verlangsamen, so dass alle irgendwann auseinander gerissen werden und auf ihren Planeten abstürzen würden. Für nicht retrogierte Satelliten implizierte ein Artikel, den ich las, dass alle das gleiche Schicksal haben werden ... Was impliziert, dass die Rotation des Planeten immer langsamer beschleunigt als die fallende Umlaufbahn des Satelliten. Ist das wahr? Wenn nicht, dann scheint es Fälle zu geben, in denen die Rotation des Planeten aufholt und sie wieder gezeitengesperrt sind.

Das ist also Frage 2: Werden alle nicht retrogierten, gezeitenverzögernden Satelliten irgendwann auf ihren Planeten stoßen, oder ist es möglich, dass der Planet unter den richtigen Startbedingungen aufholt?

Edit: Habe noch keine Informationen dazu gefunden. Gibt es jemanden, der mit relevanten Gleichungen vertraut ist und die Antwort kennt?

Das ist also Frage 1: Ist es wirklich möglich, dass die Gezeitenbeschleunigung einen Satelliten in den Weltraum wirft, bevor der Planet gezeitengesperrt ist, und wenn ja, wirkt sich entweder die Größe der Objekte darauf aus oder nur auf die Fließfähigkeit und die relativen Perioden?

Während des Verriegelungsprozesses wird der Drehimpuls des einen in den anderen eingespeist, bis die Perioden übereinstimmen. Das endgültige Ziel hängt vom Anfangsimpuls beider Objekte und dem Trägheitsmoment ab. Wenn Sie beispielsweise den Mond weniger massiv oder die Erde massereicher machen oder sich schneller drehen, hat die endgültige Konfiguration des Systems eine größere Umlaufbahn.

Sie könnten sicherlich ein System erstellen, bei dem die endgültige theoretische Konfiguration einen Abstand zum Satelliten aufweist, der jenseits der Hill-Kugel des Primärs liegt. Es wird erwartet, dass sich ein solches System irgendwann trennt.

Die Flüssigkeit kann die Geschwindigkeit ändern, mit der das endgültige Ziel erreicht wird, nicht jedoch die Konfiguration.

Werden alle nicht retrogierten, sich gezeitenverzögernden Satelliten irgendwann auf ihren Planeten stoßen, oder ist es möglich, dass der Planet unter den richtigen Startbedingungen aufholt?

Jedes Objekt überträgt den gleichen Drehimpuls. Die Reaktion jedes Objekts hängt jedoch (zumindest anfänglich) von den relativen Größen ihrer Trägheitsmomente ab. Bei einem System, bei dem der Satellit (relativ) klein ist oder bei dem der Unterschied in den Rotationsraten groß ist, sind Auswirkungen unvermeidlich. Der primäre kann nicht schnell genug beschleunigen, um mit der zunehmenden Geschwindigkeit des absteigenden Partners Schritt zu halten.

Wenn jedoch der Unterschied in den Perioden gering ist und der primäre klein genug / weit genug ist, werden die Objekte vor dem Aufprall gesperrt.

Sie haben den wichtigsten Faktor übersehen, nämlich wie nah die Sonne ist und als Ergebnis der Entfernung zur Sonne und der relativen Masse, der Hügelkugel und der ungefähren Entfernung, in der die stabile Umlaufbahn endet .

Der Drehimpuls zur Bewertung des Mondes, der vom Planeten weggeschoben wird, ist eine interessante Kombination von Formeln und könnte wahrscheinlich auf der Grundlage der von Ihnen genannten Faktoren berechnet werden: Dichte, Masse, Größe, Form und Masse der flüssigen Ozeane auf der Oberfläche, Geschwindigkeit Rotation usw. Es gibt wahrscheinlich eine nicht allzu komplexe Näherung, die für Differenzszenarien ausgearbeitet werden könnte, um zu zeigen, wie weit ein Mond wandern würde, bevor das System gezeitenweise blockiert, und wie lange es dauern würde. (Einige weniger interaktive Systeme benötigen möglicherweise Billionen oder Billiarden Jahre oder länger, um eine relativ endgültige Position zu erreichen, verglichen mit dem Zeitplan von ungefähr 50 Milliarden, den das Erd-Mond-System benötigt, um sich zu verriegeln.

Wenn wir jedoch die Sonne-Erde-Mond als Beispiel betrachten, ist das Wichtigste, ob die Erde ihren Mond verliert, wie weit sich der stabile Teil der Hügelkugel erstreckt, was, wenn die Massen aller drei Objekte so sind, wie sie sind Jetzt ist der Hauptfaktor, wie nah die Erde an der Sonne ist. Wenn die Erde so nah an der Sonne wäre wie die Venus, würde der Mond wahrscheinlich entkommen, aber es würde einige Zeit dauern. Wenn die Erde so nah an der Sonne wäre wie Merkur (im Durchschnitt), hätte sie den Mond längst verloren.

OK, ich glaube, ich habe einen einfachen Einstieg in Ihre anderen Fragen, zumindest einen guten Ausgangspunkt. Drehimpuls.

Wenn wir ein Zwei-Körper-Orbitalsystem betrachten, ist der Gezeiteneffekt auf die Umlaufbahn ziemlich einfach. Bei Systemen, bei denen sich die Ausbuchtung vor dem Mond dreht, wird der Mond langsam vom Planeten weggedrückt und die Rotation des Planeten nimmt allmählich ab.

In diesem Zweikörpersystem entkommt der Mond niemals, weil in einem Zweikörpersystem die Umlaufbahnen über eine enorme Entfernung stabil bleiben. Es stellt sich im Wesentlichen die Frage, wie weit sich der Mond entfernt und wie lange es dauert, bis das System dort gezeitengesperrt ist Zumindest mathematisch erreicht es seinen Endzustand.

Der dritte Körper auf dem Bild (die Sonne) hat verschiedene Auswirkungen. Die Beziehung zwischen der relativen Masse und Entfernung der Sonne und des Planeten bestimmt die ungefähre Grenze der stabilen Region der Hügelkugel, hinter der der Mond wahrscheinlich entweicht. Die Sonne zieht auch am Mond, was zu Störungen in seiner Umlaufbahn führt und ihn nicht krümmt, wobei sich im Vergleich dazu das Zweikörpersystem mit dem weggeschobenen Mond in Richtung Kreis bewegt.

Bei Roten Zwergen, bei denen sich Planeten in der Nähe des Sterns befinden, ist es viel wahrscheinlicher, dass der Planet gezeitenmäßig an den Stern des Roten Zwergs gebunden wird (obwohl gelegentlich eine teilweise Blockierung wie das Verhältnis von Umlaufbahn zu Rotation von Merkur von 3/2 auftreten kann), aber in den meisten Fällen In Fällen, in denen ein roter Zwergstern und Planeten relativ nahe beieinander liegen, wird der Planet tidal an den Stern gebunden und dreht sich effektiv langsamer als der Mond, was zu einer abnehmenden Umlaufbahn der Monde zu ihren Planeten in Rotzwergsystemen führt. Der stabile Orbitalbereich in solchen Systemen wäre auch viel kleiner. Die Sonne ist ein wesentlicher Faktor für die Bewegung von Monden zu oder von Planeten.

Wenn wir jedoch zum 2-Körper-System zurückkehren und den Gezeiteneffekt abschätzen, da wir wissen, dass der Mond niemals aus einem geschlossenen Zwei-Körper-System entkommen wird, stellt sich die Frage, wie weit sich der Mond vom Planeten bewegen kann und wie lange es dauern wird, bis gegenseitige Gezeitenverriegelung ist erreicht.

Wie weit der Mond vom Planeten entfernt sein kann, lässt sich anhand des gesamten Drehimpulses des Systems abschätzen. Sie haben also Recht, dass die anfängliche Rotationsgeschwindigkeit ein Faktor ist, ebenso wie die relative Masse zwischen Planet und Mond. Ein massereicherer Mond erzeugt eine größere Gezeitenwölbung auf dem Planeten, was dazu führt, dass sich der Mond schneller vom Planeten entfernt als ein weniger massereicher Mond. Gleichzeitig benötigt der massereichere Mond mehr Drehimpuls, wenn er sich vom Planeten entfernt, sodass er sich weniger weit bewegt. Ein weniger massereicher Mond bewegt sich weiter, aber es dauert viel länger, bis er dort ankommt, und es dauert auch länger, bis das Gezeitenschloss eintritt.

Ein flüssigerer Planet würde stärkere Gezeiten erfahren, was ihn wieder schneller verlangsamen würde, aber den Satelliten definitiv schneller beschleunigen würde. Eine viskosere Flüssigkeit als Wasser würde schwächere Gezeiten erfahren, aber ich denke, sie wären weiter vorne. Ich denke, mehr Flüssigkeit ist definitiv effektiver, aber es scheint weniger offensichtlich als der erste Punkt.

Es ist nicht richtig zu sagen, dass ein flüssigerer Planet stärkere Gezeiten erfahren würde. Zu sagen, dass es höhere Gezeiten geben würde, als wenn es fest wäre, wäre genauer. Die Gezeiten, die der Planet erlebt, hängen von der Masse und Entfernung des Mondes und der Größe des Planeten ab. Wenn also der Mond gleich ist, sind die Gezeiten gleich, unabhängig davon, ob der Planet flüssig oder fest ist. Flüssigkeiten sind weniger steif, daher können sie besser Gezeiten erzeugen, aber es gibt auch Gezeiten an Land. Auf der Erde werden sie Gezeiten genannt .

Die höhere Flut drückt den Mond effektiv besser und verlangsamt den Planeten schneller und Flüssigkeit reagiert effizienter auf Gezeiten, sodass Planeten mit einer flüssigen Oberfläche ihre Monde effizienter und schneller bewegen als Planeten ohne flüssige Oberfläche. Auch die Form der Ozeane spielt eine Rolle. Der breitere Pazifik hat größere Gezeiten als der engere Atlantik.

Quelle

Ich glaube nicht, dass die Viskosität der Flüssigkeit wichtig ist. Flüssigkeiten fließen, Feststoffe nicht und Vater voraus ist auch nicht korrekt. Planeten drehen sich im Allgemeinen als Einheit, obwohl es kleine Abweichungen zwischen der Rotationsrate zwischen Kern und Mantel gibt, dreht sich der gesamte Planet und die Gezeitenwölbung dreht sich mit. Flüssigkeiten sind effizienter und praller, aber in keiner Weise bewegt sich die Ausbuchtung mit der Rotation des Planeten in gleichen Winkeln vor dem Mond voran.

Ein größerer Planet würde seine Umlaufbahn durch Gezeitenbeschleunigung weniger verlangsamen, aber einen stärkeren Zug haben, um zu entkommen. Ein größerer Satellit würde stärkere Gezeiten und mehr Gezeitenkraft verursachen, würde jedoch mehr Kraft zum Beschleunigen erfordern und den Planeten schneller verlangsamen. Ich kann wirklich nicht sagen, welche die stärkere Wirkung hat ...

Hier muss man vorsichtig sein, weil es etwas komplizierter ist. Die Gezeitenkraft, die ein Planet von seinem Mond erfährt, hat mit der Masse des Mondes, der Entfernung des Mondes, aber auch mit der Masse des Planeten und dem Radius des Planeten zu tun.

Betrachten Sie die Zahlen:

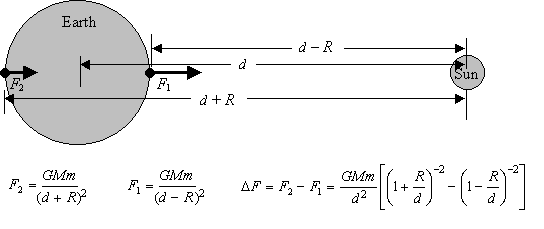
Quelle

Der 2. Teil der Formel ist ziemlich knifflig.$[(1 + R/d)^{-2} - (1 - R/d)^{-2}]$

Wenn Sie jedoch die Mathematik für ziemlich entfernte Monde berechnen, ist der Unterschied in der Gezeitenkraft von der anderen Seite des Planeten zur nahen Seite ungefähr:

Schauen Sie sich also das Erd-Mond-System an und ignorieren Sie vorerst die Sonne.

Wenn Sie die Erde gleich groß, aber doppelt so groß wie die Masse machen, verdoppelt sich die Gezeitenkraft, aber auch die Erdoberflächengravitation verdoppelt sich, wodurch das Meerwasser bei gleicher Masse doppelt so schwer wird. Die Kraft auf den Mond sollte ähnlich sein, aber eine schwerere Erde Die Verlangsamung würde länger dauern, so dass sich der Mond weiter und nicht weniger weit bewegen würde.

Wenn Sie die Dichte gleich halten und die Erde größer machen, sagen wir das 8-fache der Masse, also den doppelten Durchmesser. Die Gezeitenkraft, die der Mond auf unsere neue Supererde ausübt, wäre 16-mal größer, aber die Schwerkraft auf der Erdoberfläche nur doppelt so groß. Das bedeutet, dass sich der Mond durch die Vergrößerung des Planeten tatsächlich schneller entfernt. Der größere Planet (aber mit gleicher Dichte) sollte sich ungefähr gleich schnell verlangsamen, aber wenn sich der Mond entfernt, würde sich diese Geschwindigkeit verlangsamen.

Einige der Berechnungen zu Gezeiten werden für mich verwirrend. Die inverse Gezeitenkraft, die Monde von Planeten wegbewegt, nimmt mit der Entfernung erheblich ab. Die Gezeitenkraft fällt mit dem Würfel der Entfernung ab. Die Kraft der Gezeitenwölbung kann sogar noch schneller abfallen, da der Winkel mit der Entfernung abnimmt (ich würde vermuten, dass er mit der 4. Potenz abnimmt). Wenn sich die Entfernung des Mondes von der Erde verdoppelt, sinkt die Geschwindigkeit, mit der er sich wegbewegt von (ungefähr) 16 mal. (((Ich glaube))).

Wenn Sie also die Erde achtmal so massiv und doppelt so groß wie der Radius machen, erhöht sich die Gezeitenkraft um 16, aber wenn sich der Mond doppelt so weit bewegt, sinkt die Gezeitenkraft um 16, was ziemlich ordentlich ist, dass sie aufhebt. Das Verhältnis von Entfernung zu Schwerkraft unter der Annahme, dass sich der Mond nicht ändert und sich die Dichte des Planeten nicht ändert, beträgt 1 zu 1, was ich erwarten würde.

Das ist wahrscheinlich länger als es sein sollte und es muss wahrscheinlich viel aufgeräumt werden, aber ich muss es einen Tag nennen, also werde ich mir das morgen ansehen.